
题目列表(包括答案和解析)
已知定义在R上的函数f(x),满足条件:(1)f(x)+f(-x)=2;(2)对非零实数x,都有2f(x)+f(![]() )=2x+
)=2x+![]() +3.
+3.
(1)求函数f(x)的解析式;
(2)设函数![]() 直线
直线![]() 分别与函数g(x)的反函数y=g-1(x)交于A,B两点(其中n∈N*),设an=|AnBn|,sn为数列an的前n项和.求证:当n≥2时,总有
分别与函数g(x)的反函数y=g-1(x)交于A,B两点(其中n∈N*),设an=|AnBn|,sn为数列an的前n项和.求证:当n≥2时,总有![]() 成立.
成立.
仔细阅读下面问题的解法:
设A=[0,1],若不等式21-x+a>0在A上有解,求实数a的取值范围.
解:令f(x)=21-x+a,因为f(x)>0在A上有解。

=2+a>0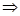 a>-2
a>-2
学习以上问题的解法,解决下面的问题,已知:函数f(x)=x2+2x+3(-2≤x≤-1).
①求f(x)的反函数f-1(x)及反函数的定义域A;
②设B=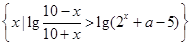 ,若A∩B≠
,若A∩B≠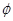 ,求实数a的取值范围.
,求实数a的取值范围.
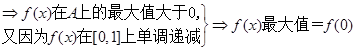
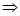 a>-2
a>-2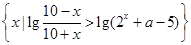 ,若A∩B≠
,若A∩B≠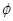 ,求实数a的取值范围.
,求实数a的取值范围.已知函数f(x)是定义在R上的偶函数,且对任意x∈R,都有f(x-1)=f(x+3).当x∈[4,6]时,f(x)=2x+1,设函数f(x)在区间[-2,0]上的反函数为f-1(x),则f-1(19)的值为
A.-log23
B.-2log23
C.1-2log23
D.3-2log23
已知函数f(x)是定义在R上的偶函数,且对任意x∈R,都有f(x-1)=f(x+3).当x∈[4,6]时,f(x)=2x+1,设函数f(x)在区间[-2,0]上的反函数为f-1(x),则f-1(19)的值为
A.-log23
B.-2log23
C.1-2log23
D.3-2log23
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com