(本小题满分16分)设数列{a_n}满足：a₁＝1，a₂＝2，a_n＋2＝(n≥1，n∈N^*)．
(1) 求证：数列是常数列；
(2) 求证：当n≥2时，2＜a－a≤3；
(3) 求a_{2 011}的整数部分.

设数列{an}满足：a1＝1，a2＝2，an＋2＝(n≥1，nÎN*)．

（1）求证：数列{}是常数列；

（2）求证：当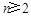时，2＜a－a≤3；

（3）求a2011的整数部分

(本小题满分13分)
设函数y＝f(x)的定义域为(0，＋∞)，且在(0，＋∞)上单调递增，若对任意x，y∈(0，＋∞)都有：f(xy)＝f(x)＋f(y)成立，数列{a_n}满足：a₁＝f(1)＋1，f(－)＋f(＋)＝0.设S_n＝aa＋aa＋aa＋…＋aa＋aa.
(1)求数列{a_n}的通项公式，并求S_n关于n的表达式；
(2)设函数g(x)对任意x、y都有：g(x＋y)＝g(x)＋g(y)＋2xy，若g(1)＝1，正项数列{b_n}满足：b＝g()，T_n为数列{b_n}的前n项和，试比较4S_n与T_n的大小.

 设函数y＝f(x)的定义域为(0，＋∞)，且在(0，＋∞)上单调递增，若对任意x，y∈(0，＋∞)都有：f(xy)＝f(x)＋f(y)成立，数列{a_n}满足：a₁＝f(1)＋1，

f(－)＋f(＋)＝0.设S_n＝aa＋aa＋aa＋…＋aa＋aa.

(1)求数列{a_n}的通项公式，并求S_n关于n的表达式；

(2)设函数g(x)对任意x、y都有：g(x＋y)＝g(x)＋g(y)＋2xy，若g(1)＝1，正项数列{b_n}满足：b＝g()，T_n为数列{b_n}的前n项和，试比较4S_n与T_n的大小.