已知函数，.

（Ⅰ）若函数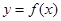依次在处取到极值.求的取值范围；

（Ⅱ）若存在实数，使对任意的，不等式 恒成立.求正整数的最大值.

【解析】第一问中利用导数在在处取到极值点可知导数为零可以解得方程有三个不同的实数根来分析求解。

第二问中，利用存在实数，使对任意的，不等式 恒成立转化为，恒成立，分离参数法求解得到范围。

解：（1）

①

（2）不等式 ，即，即.

转化为存在实数，使对任意的，不等式恒成立.

即不等式在上恒成立.

即不等式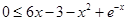在上恒成立.

设，则.

设，则，因为，有.

故在区间上是减函数。又

故存在，使得.

当时，有，当时，有.

从而在区间上递增，在区间上递减.

又[来源:]

所以当时，恒有；当时，恒有；

故使命题成立的正整数m的最大值为5

 

某校从参加高三年级理科综合物理考试的学生中随机抽出名学生，将其数学成绩（均为整数）分成六段，…后得到如下部分频率分布直方图.观察图形的信息，回答下列问题：

（Ⅰ）求分数在内的频率，并补全这个频率分布直方图；

（Ⅱ）统计方法中，同一组数据常用该组区间的中点值作为代表，据此估计本次考试的

平均分；

（Ⅲ）若从名学生中随机抽取人，抽到的学生成绩在记分，在记分，

在记分，用表示抽取结束后的总记分，求的分布列和数学期望.

【解析】（1）中利用直方图中面积和为1，可以求解得到分数在内的频率为

（2）中结合平均值可以得到平均分为：

（3）中用表示抽取结束后的总记分x, 学生成绩在的有人，在的有人，在的有人,结合古典概型的概率公式求解得到。

(Ⅰ)设分数在内的频率为，根据频率分布直方图，则有，可得，所以频率分布直方图如右图.……4分

（求解频率3分，画图1分）

（Ⅱ）平均分为：……7分

（Ⅲ）学生成绩在的有人，在的有人，

在的有人.并且的可能取值是.    ………8分

则；； ；

；.（每个1分）

所以的分布列为

	0	1	2	3	4

…………………13分