
题目列表(包括答案和解析)
定义在R上的函数f(x)满足f(x+y)=f(x)+f(y)+2xy(x,y∈R),f(1)=2,则f(-3)等于( )
A.2 B.3
C.6 D.9
![]() 定义在R上的函数f(x)满足f(x)=
定义在R上的函数f(x)满足f(x)=![]() ,则f(-1)=______
,则f(-1)=______![]() __,f(33)=________.
__,f(33)=________.
定义在R上的函数f(x)满足f(x)+f(x+5)=16,当x∈(-1,4]时,f(x)=x2-2x,则函数f(x)在[0,2013]上的零点个数是_____ .
定义在R上的函数f(x)满足f(4)=1,f′(x)为函数f(x)的导函数.已知函数y=f′(x)的图象如图所示,两个正数a、b满足f(2a+b)<1,则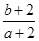 的取值范围是( )
的取值范围是( )
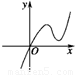
(A)(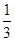 ,
,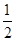 ) (B)(-∞,
) (B)(-∞,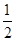 )∪(3,+∞) (C)(
)∪(3,+∞) (C)(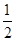 ,3) (D)(-∞,-3)
,3) (D)(-∞,-3)
定义在R上的函数f(x)满足f(x+2)=3f(x),当x∈[0,2]时,f(x)=x2-2x,则当x∈[-4,-2]时,f(x)的最小值是( )
A.-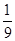 B.-
B.-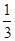 C.
C. 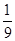 D.-1
D.-1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com