（08年鹰潭市二模理）有以下几个命题

 ①曲线按平移可得曲线；

②直线AB与平面相交于点B，且AB与内相交于点C的三条互不重合的直线CD、CE、CF所成的角相等，则AB⊥；

③已知椭圆与双曲线有相同的准线，则动点的轨迹为直线

④若直线在平面内的射影依次为一个点和一条直线，且，则；

⑤设A、B为平面上两个定点，P为动点，若，则动点P的轨迹为圆

其中真命题的序号为               ;（写出所有真命题的序号）　

如图，平面直角坐标系中，点A、B、C在x轴上，点D、E在y轴上，OA=OD=2，

OC=OE=4，DB⊥DC，直线AD与经过B、E、C三点的抛物线交于F、G两点，与其对称轴交

于M.点P为线段FG上一个动点(与F、G不重合)，PQ∥y轴与抛物线交于点Q.

(1)求经过B、E、C三点的抛物线的解析式；

(2)是否存在点P，使得以P、Q、M为顶点的三角形与△AOD相似？若存在，求出满足条件

的点P的坐标；若不存在，请说明理由；

(3)若抛物线的顶点为N，连接QN，探究四边形PMNQ的形状：①能否成为菱形；②能否成

为等腰梯形？若能，请直接写出点P的坐标；若不能，请说明理由.

如图，平面直角坐标系中，点A、B、C在x轴上，点D、E在y轴上，OA=OD=2，
OC=OE=4，DB⊥DC，直线AD与经过B、E、C三点的抛物线交于F、G两点，与其对称轴交
于M.点P为线段FG上一个动点(与F、G不重合)，PQ∥y轴与抛物线交于点Q.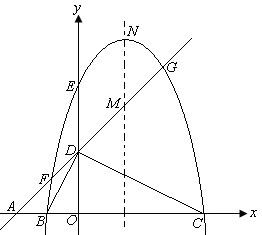

(1)求经过B、E、C三点的抛物线的解析式；
(2)是否存在点P，使得以P、Q、M为顶点的三角形与△AOD相似？若存在，求出满足条件
的点P的坐标；若不存在，请说明理由；
(3)若抛物线的顶点为N，连接QN，探究四边形PMNQ的形状：①能否成为菱形；②能否成
为等腰梯形？若能，请直接写出点P的坐标；若不能，请说明理由.