
题目列表(包括答案和解析)
设平面上的动向量![]() ,其中
,其中![]() 为不同时为0的两个实数,实数
为不同时为0的两个实数,实数![]() ,满足
,满足![]()
(1)求函数关系式![]() ;
;
(2)若函数![]() 在
在![]() 上单调递增,求
上单调递增,求![]() 的范围;
的范围;
(3)对上述![]() ,当
,当![]() 时,存在正项数列
时,存在正项数列![]() 满足
满足![]() ,其中
,其中![]() ,证明:
,证明: ![]() <3
<3
设平面上的动向量![]() ,
,![]() ,其中s、t为不同时为0的两个实数,实数
,其中s、t为不同时为0的两个实数,实数![]() ,满足
,满足![]() 。
。
(1)求函数关系式![]() ;
;
(2)若函数![]() 在
在![]() 上单调递增,求
上单调递增,求![]() 的范围;
的范围;
(3)对上述![]() ,当
,当![]() 时,存在正项数列
时,存在正项数列![]() 满足
满足![]() ,其中
,其中![]() ,证明:
,证明: 。
。
设函数![]()
![]()
(Ⅰ)若![]() 时函数
时函数![]() 有三个互不相同的零点,求
有三个互不相同的零点,求![]() 的范围;
的范围;
(Ⅱ)若函数![]() 在
在![]() 内没有极值点,求
内没有极值点,求![]() 的范围;
的范围;
(Ⅲ)若对任意的![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
已知函数
(Ⅰ)若函数f(x)在[1,2]上是减函数,求实数a的取值范围;
(Ⅱ)令g(x)= f(x)-x2,是否存在实数a,当x∈(0,e](e是自然常数)时,函数g(x)的最小值是3,若存在,求出a的值;若不存在,说明理由;
(Ⅲ)当x∈(0,e]时,证明:
【解析】本试题主要是考查了导数在研究函数中的运用。第一问中利用函数f(x)在[1,2]上是减函数,的导函数恒小于等于零,然后分离参数求解得到a的取值范围。第二问中,
假设存在实数a,使 有最小值3,利用
有最小值3,利用 ,对a分类讨论,进行求解得到a的值。
,对a分类讨论,进行求解得到a的值。
第三问中,
因为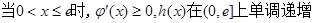 ,这样利用单调性证明得到不等式成立。
,这样利用单调性证明得到不等式成立。
解:(Ⅰ) 
(Ⅱ) 
(Ⅲ)见解析
 (2013•肇庆二模)PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.虽然PM2.5只是地球大气成分中含量很少的组分,但它对空气质量和能见度等有重要的影响.我国PM2.5标准如表1所示.我市环保局从市区四个监测点2012年全年每天的PM2.5监测数据中随机抽取15天的数据作为样本,监测值如茎叶图如图所示.
(2013•肇庆二模)PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.虽然PM2.5只是地球大气成分中含量很少的组分,但它对空气质量和能见度等有重要的影响.我国PM2.5标准如表1所示.我市环保局从市区四个监测点2012年全年每天的PM2.5监测数据中随机抽取15天的数据作为样本,监测值如茎叶图如图所示.| PM2.5日均值(微克/立方米)范围 | 空气质量级别 |
| (1,35] | I |
| (35,75] | II |
| 大于75 | 超标 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com