
题目列表(包括答案和解析)
| x | 16 | 20 | 24 | 28 |
| y | 42 | 30 | 18 | 6 |
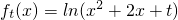 是思法函数,且不等式2t+1+3t+1≤k(2t+3t)对所有的ft(x)都成立,求实数k的取值范围.
是思法函数,且不等式2t+1+3t+1≤k(2t+3t)对所有的ft(x)都成立,求实数k的取值范围.已知指数函数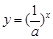 ,当
,当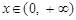 时,有
时,有 ,解关于x的不等式
,解关于x的不等式
【解析】本试题主要考查了指数函数,对数函数性质的运用。首先利用指数函数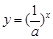 ,当
,当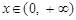 时,有
时,有 ,,得到
,,得到 ,从而
,从而
 等价于
等价于 ,联立不等式组可以解得
,联立不等式组可以解得
解:∵ 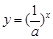 在
在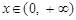 时,有
时,有 ,
∴
,
∴  。
。
于是由 ,得
,得 ,
,
解得 ,
∴ 不等式的解集为
,
∴ 不等式的解集为 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com