题目列表(包括答案和解析)
| A．函数只要有零点，就能用二分法求 |
| B．零点是整数的函数不能用二分法求 |
| C．多个零点的函数，不能用二分法求零点的近似解 |
| D．以上说法都错误 |
（本小题满分9分）
以下是用二分法求方程
的一个近似解（精确度为0.1）的不完整的过程，请补充完整。
| 区间 | 中点 |
| 区间长度 |
解：设函数
，
其图象在上是连续不
断的，且
在上是
单调递______（增或减）。
先求
_______，
______，
____________。
所以在区间____________内存在零点
，再填上表：
下结论：_______________________________。
（可参考条件：
，
；符号填＋、－）
用二分法求函数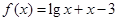
的一个零点，其参考数据如下：
|
f(2)≈-0.699 |
f(3) ≈0.477 |
f(2.5) ≈-0.102 |
f(2.75) ≈0.189 |
|
f(2.625) ≈0.044 |
f(2.5625)≈-0.029 |
f(2.59375)≈0.008 |
f(2.57813≈-0.011 |
根据此数据，可得方程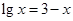
的一个近似解（精确到0.1）为
用二分法求函数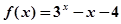
的一个零点，其参考如下数据：
|
|
|
|
|
|
|
|
由此可得到的方程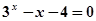
的一个近似解（精确到
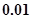）为
. 
. 
. 
. 
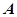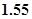
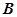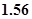
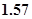
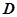湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
符号
