
题目列表(包括答案和解析)
(1)证明a>0,c>0;
(2)设函数g(x)=f(x)-mx(x∈R),求m的取值范围,使函数g(x)在区间[-1,1]上是单调函数.
(1)设二次函数f ( x ) = ax2 + bx + c,证明 f ( x ) > 0对一切x∈R恒成立的充要条件是a > 0,且Δ= b2-4ac < 0;
(2)设a1,a2,…,an,b1,b2,…,bn是不全为零的任意实数,利用(1)的结论证明:![]() .
.
(2)设a1,a2,…,an,b1,b2,…,bn是不全为零的任意实数,利用(1)的结论证明:![]() .
.
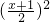 .
. .
.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com