
题目列表(包括答案和解析)
(本小题满分14分)如果对于函数![]() 的定义域内任意的
的定义域内任意的![]() ,都有
,都有![]() 成立,那么就称函数
成立,那么就称函数![]() 是定义域上的“平缓函数”.
是定义域上的“平缓函数”.
(1)判断函数![]() ,
,![]() 是否是“平缓函数”;(2)若函数
是否是“平缓函数”;(2)若函数![]() 是闭区间
是闭区间![]() 上的“平缓函数”,且
上的“平缓函数”,且![]() .证明:对于任意的
.证明:对于任意的![]()
![]() ,都有
,都有![]() 成立.(3)设
成立.(3)设![]() 、
、![]() 为实常数,
为实常数,![]() .若
.若![]() 是区间
是区间![]() 上的“平缓函数”,试估计
上的“平缓函数”,试估计![]() 的取值范围(用
的取值范围(用![]() 表示,不必证明).
表示,不必证明).
如果对于函数![]() 的定义域内任意的
的定义域内任意的![]() ,都有
,都有![]() 成立,那么就称函数
成立,那么就称函数![]() 是定义域上的“平缓函数”.(1)判断函数
是定义域上的“平缓函数”.(1)判断函数![]() ,
,![]() 是否是“平缓函数”;(2)若函数
是否是“平缓函数”;(2)若函数![]() 是闭区间
是闭区间![]() 上的“平缓函数”,且
上的“平缓函数”,且![]() .证明:对于任意的
.证明:对于任意的![]()
![]() ,都有
,都有![]() 成立.(3)设
成立.(3)设![]() 、
、![]() 为实常数,
为实常数,![]() .若
.若![]() 是区间
是区间![]() 上的“平缓函数”,试估计
上的“平缓函数”,试估计![]() 的取值范围(用
的取值范围(用![]() 表示,不必证明).
表示,不必证明).
如果对于函数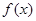 的定义域内任意一个
的定义域内任意一个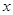 的值,均有
的值,均有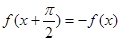 ,且
,且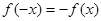 ,对于下列五个函数:①
,对于下列五个函数:①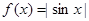 ;②
;②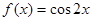 ; ③
; ③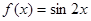 ;④
;④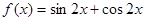 ,其中适合题设条件的函数的序号是 .
,其中适合题设条件的函数的序号是 .
如果对于函数 的定义域内任意两个自变量的值
的定义域内任意两个自变量的值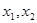 ,当
,当 时,都有
时,都有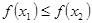 且存在两个不相等的自变量
且存在两个不相等的自变量 ,使得
,使得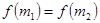 ,则称
,则称 为定义域上的不严格的增函数.已知函数
为定义域上的不严格的增函数.已知函数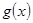 的定义域、值域分别为
的定义域、值域分别为 ,
,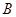 ,
, ,
,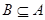 且
且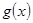 为定义域
为定义域 上的不严格的增函数,那么这样的函数
上的不严格的增函数,那么这样的函数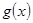 共有________个.
共有________个.
(本小题满分14分) 如果对于函数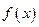 的定义域内的任意
的定义域内的任意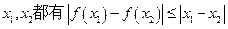 成立,那么就称函数
成立,那么就称函数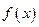 是定义域上的“平缓函数”.
是定义域上的“平缓函数”.
(1)判断函数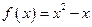 ,
,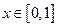 是否是 “平缓函数”?
是否是 “平缓函数”?
(2)若函数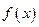 是闭区间
是闭区间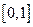 上的“平缓函数”,且
上的“平缓函数”,且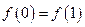 .证明:对任意的
.证明:对任意的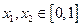 都有
都有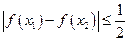 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com