练习册

  • 练习册
  • 试题
    19．甲.乙两人约定在下午1点到2点之间到某汽车站乘公共汽车．又这段时间内有4班公共汽车.它们的开车时刻分别为1∶15,1∶30,1∶45.2∶00.已知甲.乙到达车站的时刻是互相不牵连的.且每人在1点到2点的任何时刻到达车站是等可能的． (1)如果他们约定见车就乘.求甲.乙同乘一辆车的概率, (2)如果他们约定最多等一辆车.求甲.乙同乘一辆车的概率． 解:设x.y(1≤x≤2,1≤y≤2)分别为甲.乙到达的时刻．P为甲乙同乘一辆车的概率． (1)见车就上的情况如图(1)所示． P＝＝＝. (2)法一:最多等一辆车的情况下.甲乙同乘一车包括3种情况:见车就上,甲先到达等一辆车然后与乙同乘一辆车,乙先到达等一辆车.然后与甲同乘一车． P＝+×2＝. 法二:如图(3).P＝＝. 【查看更多】

     

    题目列表(包括答案和解析)

    （本小题满分12分）

    甲乙两人进行围棋比赛，约定每局胜者得1分，负者得分，比赛进行到有一人比对方多分或打满局时停止．设甲在每局中获胜的概率为，且各局胜负相互独立．已知第二局比赛结束时比赛停止的概率为．

    （1）求的值；

    （2）设表示比赛停止时已比赛的局数，求随机变量的分布列和数学期望．

    查看答案和解析>>

    （本小题满分12分）

    甲乙两人进行围棋比赛，约定每局胜者得1分，负者得分，比赛进行到有一人比对方多分或打满局时停止．设甲在每局中获胜的概率为，且各局胜负相互独立．已知第二局比赛结束时比赛停止的概率为．

    （1）求的值；

    （2）设表示比赛停止时已比赛的局数，求随机变量的分布列和数学期望．

    查看答案和解析>>

    （本小题满分12分）

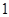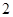    甲，乙两人进行乒乓球比赛，约定每局胜者得分，负者得分，比赛进行到有一人比对方多分或打满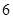局时停止．设甲在每局中获胜的概率为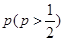，且各局胜负相互独立．若第二局比赛结束时比赛停止的概率为．

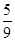    （1）求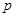的值；

    （2）设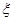表示比赛停止时比赛的局数，求随机变量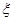的分布列和数学期望。

     

    查看答案和解析>>

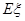    （本小题满分12分）

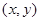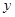    某市地铁全线共有四个车站，甲、乙两人同时在地铁第一号车站(首发站)乘车.假设每人自第2号车站开始,在每个车站下车是等可能的。约定用有序实数对表示“甲在号车站下车，乙在号车站下车”．

    （1）用有序实数对把甲、乙两人下车的所有可能的结果列举出来；

    （2）求甲、乙两人同在第3号车站下车的概率；

    （3）求甲、乙两人在不同的车站下车的概率．

     

    查看答案和解析>>

    （本小题满分12分）
    甲，乙两人进行乒乓球比赛，约定每局胜者得分，负者得分，比赛进行到有一人比对方多分或打满局时停止．设甲在每局中获胜的概率为，且各局胜负相互独立．若第二局比赛结束时比赛停止的概率为．
    （1）求的值；
    （2）设表示比赛停止时比赛的局数，求随机变量的分布列和数学期望。

    查看答案和解析>>


    同步练习册答案