
题目列表(包括答案和解析)
(本题满分10)如图所示,已知AB为⊙O的直径,AC为弦,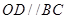 ,交AC于点D,BC=4cm,
,交AC于点D,BC=4cm,
(1)求OD的长;
(2)若 ,求⊙O的直径.
,求⊙O的直径.
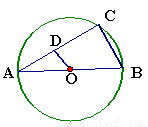
(本题满分10)如图所示,已知AB为⊙O的直径,AC为弦,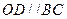 ,交AC于点D,BC=4cm,
,交AC于点D,BC=4cm,
(1)求OD的长;
(2)若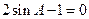 ,求⊙O的直径.
,求⊙O的直径.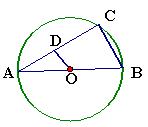
质量
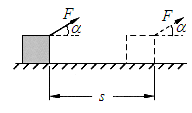
m=2.0kg的物体,受到与水平方向夹角为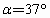 的斜向上拉力F的作用,沿水平面移动了s=1.0m的距离(如图所示),已知F=10N,物体受到的摩擦力是它与水平面间压力的0.2倍,求力F对物体做的功.(取g=10m/
的斜向上拉力F的作用,沿水平面移动了s=1.0m的距离(如图所示),已知F=10N,物体受到的摩擦力是它与水平面间压力的0.2倍,求力F对物体做的功.(取g=10m/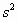 ,
,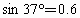 ,
,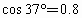 )
)
 11、为了了解噪声污染的情况,某市环保局抽样调查了80个测量点的噪声声级(单位:分贝),并进行整理后分成五组,绘制出频率分布直方图,如图所示.已知从左至右前四组的频率分别是0.15,0.25,0.3,0.2,且噪声声级高于69.5分贝就会影响工作和生活,那么影响到工作和生活而需对附近区域进行治理的测量点有( )
11、为了了解噪声污染的情况,某市环保局抽样调查了80个测量点的噪声声级(单位:分贝),并进行整理后分成五组,绘制出频率分布直方图,如图所示.已知从左至右前四组的频率分别是0.15,0.25,0.3,0.2,且噪声声级高于69.5分贝就会影响工作和生活,那么影响到工作和生活而需对附近区域进行治理的测量点有( )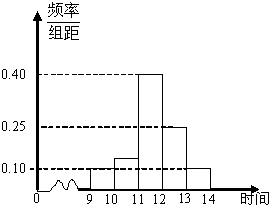 某商场在国庆黄金周的促销活动中,对10月2日9时到14时的销售额进行统计,其频率分布直方图如图所示,已知9时至10时的销售额为2.5万元,则11时到12时的销售额为( )
某商场在国庆黄金周的促销活动中,对10月2日9时到14时的销售额进行统计,其频率分布直方图如图所示,已知9时至10时的销售额为2.5万元,则11时到12时的销售额为( )| A、6万元 | B、8万元 | C、10万元 | D、12万元 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com