
题目列表(包括答案和解析)
| |||||||||||||||
下列推理中属于归纳推理且结论正确的是( )
A.设数列{an}的前n项和为Sn.由an=2n-1,求出S1=12,S2=22,S3=32,…,推断:Sn=n2
B.由f(x)=xcos x满足f(-x)=-f(x)对?x∈R都成立,推断:f(x)=xcos x为奇函数
C.由圆x2+y2=r2的面积S=πr2,推断:椭圆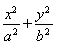 =1(a>b>0)的面积S=πab
=1(a>b>0)的面积S=πab
D.由(1+1)2>21,(2+1)2>22,(3+1)2>23,…,推断:对一切n∈N*,(n+1)2>2n
| A.设数列{an}的前n项和为Sn.由an=2n-1,求出S1=12,S2=22,S3=32,…,推断:Sn=n2 |
| B.由f(x)=xcos x满足f(-x)=-f(x)对?x∈R都成立,推断:f(x)=xcos x为奇函数 |
C.由圆x2+y2=r2的面积S=πr2,推断:椭圆 =1(a>b>0)的面积S=πab =1(a>b>0)的面积S=πab |
| D.由(1+1)2>21,(2+1)2>22,(3+1)2>23,…,推断:对一切n∈N*,(n+1)2>2n |
下列推理中属于归纳推理且结论正确的是( )
| A.设数列{an}的前n项和为Sn.由an=2n-1,求出S1=12,S2=22,S3=32,…,推断:Sn=n2 |
| B.由f(x)=xcos x满足f(-x)=-f(x)对?x∈R都成立,推断:f(x)=xcos x为奇函数 |
C.由圆x2+y2=r2的面积S=πr2,推断:椭圆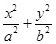 =1(a>b>0)的面积S=πab =1(a>b>0)的面积S=πab |
| D.由(1+1)2>21,(2+1)2>22,(3+1)2>23,…,推断:对一切n∈N*,(n+1)2>2n |
下列推理是归纳推理的是
A.A,B为两个定点,动点P满足||PA|-|PB||=2a<|AB|,(a>0),则动点P的轨迹是以A,B为焦点的双曲线;
B.由a1=2,an=3n-1,求出S1,S2,S3,猜想出数列{an}的前n项和Sn的表达式;
C.由圆x2+y2=r2的面积S=πr2,猜想出椭圆![]() 的面积S=πab;
的面积S=πab;
D.科学家利用鱼的沉浮原理制造潜水艇.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com