
题目列表(包括答案和解析)
下列四类函数中,有“对定义域内任意的实数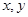 ,函数
,函数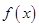 满足
满足
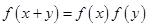 ”的是
(
)
”的是
(
)
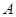 .幂函数
.幂函数 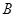 .对数函数
.对数函数
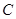 .指数函数
.指数函数
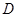 .余弦函数
.余弦函数
下列四类函数中,有“对定义域内任意的实数 ,函数
,函数 满足
满足
 ”的是
(
)
”的是
(
)
 .幂函数
.幂函数  .对数函数
.对数函数
 .指数函数
.指数函数
 .余弦函数
.余弦函数
某企业科研课题组计划投资研发一种新产品,根据分析和预测,能获得10万元~1000万元的投资收益.企业拟制定方案对课题组进行奖励,奖励方案为:奖金![]() (单位:万元)随投资收益
(单位:万元)随投资收益![]() (单位:万元)的增加而增加,且奖金不超过9万元,同时奖金也不超过投资收益的20%,并用函数
(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金也不超过投资收益的20%,并用函数![]() 模型模拟这一奖励方案.
模型模拟这一奖励方案.
(I)试写出模拟函数![]() 所满足的条件;
所满足的条件;
(II)试分析下列两个函数模型是否符合奖励方案的要求?并说明你的理由.
①![]() , ②
, ②![]() .
.
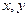 ,函数
,函数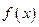 满足
满足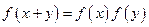 ”的是 ( )
”的是 ( )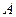 .幂函数
.幂函数 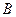 .对数函数
.对数函数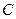 .指数函数
.指数函数 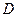 .余弦函数
.余弦函数| t | 1.99 | 3.0 | 4.0 | 5.1 | 6.12 |
| u | 1.5 | 4.04 | 7.5 | 12 | 18.01 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com