练习册

  • 练习册
  • 试题
    1．一次函数模型:, 【查看更多】

     

    题目列表(包括答案和解析)

    解题过程中究竟选用哪种函数模型，要根据题目具体要求进行抽象和概括，灵活地选取和建立数学模型，常用的数学模型有：

    (1)一次函数模型，其形式为________；

    (2)二次函数模型，其形式为________；

    (3)指数函数模型，其形式为________；

    (4)对数函数模型，其形式为________；

    (5)幂函数模型，其形式为________．

    查看答案和解析>>

    某汽车公司曾在2009年初公告：2009年销量目标定为39.3万辆；且该公司董事长极力表示有信心完成这个销量目标．
    2006年，某汽车年销量8万辆；
    2007年，某汽车年销量18万辆；
    2008年，某汽车年销量30万辆．
    如果我们分别将2006，2007，2008，2009年定义为第一，二，三，四年，现在有两个函数模型：二次函数型f(x)=ax2+bx+c(a≠0)，指数函数型g(x)=a·bx+c(a≠0，b≠1，b＞0)，哪个模型能更好地反映该公司年销量y与第x年的关系？

    查看答案和解析>>

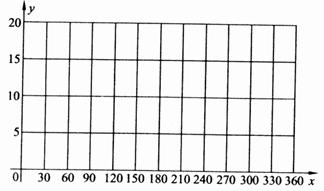
    在自然条件下，一年中10次测量的某种细菌一天内存活时间的统计表（时间近似到0.1小时）如下表所示：

    日期

    1月

    1日

    2月

    28日

    3月

    21日

    4月

    27日

    5月

    27日

    6月

    21日

    8月

    13日

    9月

    20日

    10月

    25日

    12月

    21日

    日期位置序号x

    1

    59

    80

    117

    126

    172

    225

    263

    298

    355

    存活时间y（小时）

    5.6

    10.2

    12.3

    16.4

    17.3

    19.4

    16.4

    12.5

    8.5

    5.4

    （1）       以日期在365天中的位置序号为横坐标，一天内存活时间为纵坐标，在给定坐标系中画出这些数据的散点图.

    （2）       试选用一个形如+t的函数来近似描述一年中该细菌一天内的存活时间y与日期位置序号x之间的函数关系.（注：①求出所选用的函数关系式；②一年按365天计算）

    （3）       用（2）中的函数模型估计该种细菌一年中大约有多少天的存活时间大于15.9小时.

    查看答案和解析>>


    同步练习册答案