
题目列表(包括答案和解析)
定理:如果函数y=f(x)在区间[a,b]上的图象是________的一条曲线,并且有f(a)·f(b)________0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)________0,这个c也就是方程f(x)=0的根.
| x2 | 6 |
 和y=|log2x|的图象的交点有且只有一个;
和y=|log2x|的图象的交点有且只有一个;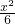 和y=|log2x|的图象的交点有且只有一个;
和y=|log2x|的图象的交点有且只有一个;湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com