
题目列表(包括答案和解析)
平面内与两定点 、
、
 连线的斜率之积等于非零常数
连线的斜率之积等于非零常数 的点的轨迹,加上
的点的轨迹,加上 、
、 两点所成的曲线
两点所成的曲线 可以是圆、椭圆或双曲线。求曲线
可以是圆、椭圆或双曲线。求曲线 的方程,并讨论
的方程,并讨论 的形状与
的形状与 值的关系。
值的关系。
【解析】本试题主要考查了平面中动点的轨迹方程,利用斜率之积为定值可以对参数进行分类讨论,并得到关于不同曲线的参数的范围问题。对于方程的特点做了很好的考查和运用。
平面内与两定点 、
、
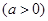 连线的斜率之积等于非零常数
连线的斜率之积等于非零常数 的点的轨迹,加上
的点的轨迹,加上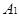 、
、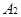 两点所成的曲线
两点所成的曲线 可以是圆、椭圆或双曲线。求曲线
可以是圆、椭圆或双曲线。求曲线 的方程,并讨论
的方程,并讨论 的形状与
的形状与 值的关系。
值的关系。
【解析】本试题主要考查了平面中动点的轨迹方程,利用斜率之积为定值可以对参数进行分类讨论,并得到关于不同曲线的参数的范围问题。对于方程的特点做了很好的考查和运用。
利用存在性命题、全称命题求参数的范围或值:
函数f(x)对一切实数x、y均有f(x+y)-f(y)=(x+2y+1)x成立,且f(1)=0.
(1)求f(0)的值;
(2)当f(x)+2<logax,x∈(0,![]() )恒成立时,求a的取值范围.
)恒成立时,求a的取值范围.
探究:此命题为全称命题,对x,y赋值有一定的技巧性.另外本题还要对参数a分类讨论.
| ? |
| y |
| ? |
| y |
A.20°
B.70°
C.110°
D.160°
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com