
题目列表(包括答案和解析)
某社区的常住人口中,有成年人3200人,其中有无业人员1000人,从事个体劳动的有1160人,有固定收入的上班人员1040人,如果想通过调查其中160人的生活消费情况来了解本社区群众的生活消费情况,考虑到由于各种人员情况的差异,而同一阶层人员的差异较小,问应当采取怎样的抽取方法?从事个体劳动的人员中应抽查多少人?在本问题的设计中还有哪些重要因素将影响调查效果?应怎样改进抽查方案使效果更加客观?
对于函数 ,若存在实数对(
,若存在实数对( ),使得等式
),使得等式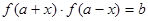 对定义域中的每一个
对定义域中的每一个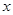 都成立,则称函数
都成立,则称函数 是“(
是“( )型函数”.
)型函数”.
(1) 判断函数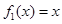 是否为“(
是否为“( )型函数”,并说明理由;
)型函数”,并说明理由;
(2) 若函数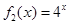 是“(
是“( )型函数”,求出满足条件的一组实数对
)型函数”,求出满足条件的一组实数对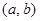 ;
;
(3)已知函数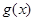 是“(
是“( )型函数”,对应的实数对
)型函数”,对应的实数对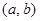 为(1,4).当
为(1,4).当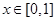 时,
时,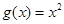
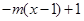
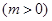 ,若当
,若当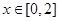 时,都有
时,都有 ,试求
,试求 的取值范围.
的取值范围.
四个变量 ,
, ,
,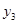 ,
,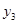 随变量
随变量 变化的数据如下表:
变化的数据如下表:
 | 0 | 5 | 10 | 15 | 20 | 25 |
 | 5 | 130 | 505 | 1130 | 2005 | 3130 |
 | 5 | 94.478 | 1785.2 | 33733 | 6.37 | 1.2 |
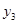 | 5 | 30 | 55 | 80 | 105 | 130 |
 | 5 | 2.3107 | 1.4295 | 1.11407 | 1.0461 | 1.0151 |
 呈指数型函数变化的变量是( )
呈指数型函数变化的变量是( ) B.
B. C.
C.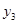 D.
D.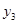
对于函数 ,若存在实数对(
,若存在实数对( ),使得等式
),使得等式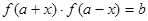 对定义域中的每一个
对定义域中的每一个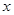 都成立,则称函数
都成立,则称函数 是“(
是“( )型函数”.
)型函数”.
(Ⅰ)判断函数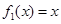 是否为 “(
是否为 “( )型函数”,并说明理由;
)型函数”,并说明理由;
(Ⅱ)若函数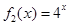 是“(
是“( )型函数”,求出满足条件的一组实数对
)型函数”,求出满足条件的一组实数对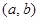 ;,
;,
(Ⅲ)已知函数 是“(
是“( )型函数”,对应的实数对
)型函数”,对应的实数对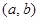 为
为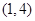 .当
.当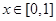 时,
时,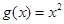
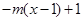
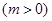 ,若当
,若当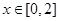 时,都有
时,都有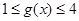 ,试求
,试求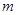 的取值范围.
的取值范围.
x | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
y1 | 5 | 130 | 505 | 1 130 | 2 005 | 3 130 | 4 505 |
y2 | 5 | 94.478 | 1 785.23 | 3 733 | 6.37×105 | 1.2×107 | 2.28×108 |
y3 | 5 | 30 | 55 | 80 | 105 | 130 | 155 |
y4 | 5 | 2.310 7 | 1.429 5 | 1.140 7 | 1.046 1 | 1.015 1 | 1.005 |
关于x呈指数型函数变化的变量是____________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com