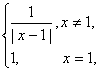设定义域为R的函数f(x)=.若关于x的方程f²(x)＋bf(x)＋c=0有3个不同的实数解x₁、x₂、x ₃，则x₁²+x₂²+x₃²等于（    ）

A.5               B.             C.13              D.

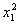设定义域为R的函数f(x)=若关于x的方程f²(x)+bf(x)+c=0有3个不同的实数解x₁、x₂、x₃,则++x²₃等于（    ）

A.5             B.              C.13              D.

定义域为R的函数f(x)=若方程f²(x)+bf(x)+c=0有且只有3个不同的实数根x₁、x₂、x₃，则x₁+x₂+x₃=________________.

设函数f(x)的定义域为D，若存在非零实数l使得对于任意x∈M(M⊆D)，有x＋l∈D，且f(x＋l)≥f(x)，则称f(x)为M上的l高调函数.

(1)如果定义域为[－1，＋∞)的函数f(x)＝x²为[－1，＋∞)上的m高调函数，求实数m的取值范围.

(2)如果定义域为R的函数f(x)是奇函数，当x≥0时，f(x)＝|x－a²|－a²，且f(x)为R上的4高调函数，求实数a的取值范围.

设定义域为R的函数f(x)满足下列条件：①对任意x∈R，f(x)＋f(－x)＝0；②对任意x∈[－1,1]，都有>0，且f(－1)＝－1.若函数f(x)≤t²－2at＋1对所有的x∈[－1,1]都成立，则当a∈[－1,1]时，t的取值范围是(　　)

A．－2≤t≤2

B．t≤－或t＝0或t≥

C．－≤t≤

D．t≤－2或t＝0或t≥2