
题目列表(包括答案和解析)
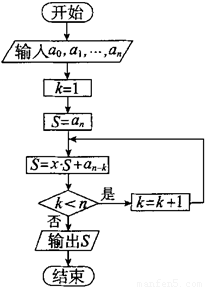
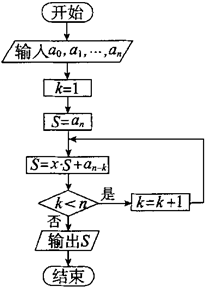 已知n次多项式Sn(x)=
已知n次多项式Sn(x)=| n |
 |
| i=0 |
| n(n+3) |
| 2 |
| n(n+3) |
| 2 |
设A={x||x-1|<2},B={x|![]() >0},则A∩B等于
>0},则A∩B等于
A.{x|-1<x<3} B.{x|x<0或x>2}
C.{x|-1<x<0} D.{x|-1<x<0或2<x<3}
本题考查含绝对值不等式、分式不等式的解法及集合的运算.在进行集合运算时,把解集标在数轴上,借助图形可直观求解.
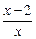 >0},则A∩B等于
>0},则A∩B等于| A.{x|-1<x<3} | B.{x|x<0或x>2} |
| C.{x|-1<x<0} | D.{x|-1<x<0或2<x<3} |
 .
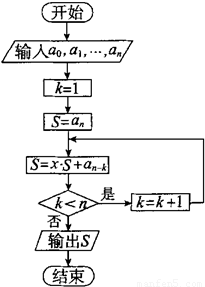
.
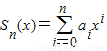 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com