
题目列表(包括答案和解析)
补集是以“全集”为前提而建立的概念,而全集又是相对于所研究的问题而言的一个概念;只要包含研究问题的全体元素的集合都可作为________.
如图,弹簧挂着小球作上下振动,时间t(s)与小球相对于平衡位置(即静止时的位置)的高度h(cm)之间的函数关系式是![]() ,t∈[0,+∞).以t为横坐标,h为纵坐标,画出这个函数在长度为一个周期的闭区间上的简图,并且回答下列问题:
,t∈[0,+∞).以t为横坐标,h为纵坐标,画出这个函数在长度为一个周期的闭区间上的简图,并且回答下列问题:
(1)小球开始振动(t=0)时位置在哪里?
(2)小球最高点、最低点与平衡位置的距离分别是多少?
(3)小球往复振动一次需要多长时间?
(4)小球每1 s能往复振动多少次?
如图,挂在弹簧下方的小球做上下振动,小球在时间
t(s)时相对于平衡位置(即静止的位置)的高度为h(单位:cm),由下列关系式决定: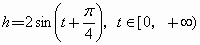 .
.
以横轴表示时间,纵轴表示高度,作出这个函数在长度为一个周期的闭区间上的简图,并回答下列问题:
(1)
小球开始振动(t=0)时的位置在哪里?(2)
小球位于最高、最低位置时h的值是多少?(3)
经过多少时间小球振动一次(即周期是多少)?(4)
小球每1s能往复振动多少次(即频率是多少)?| x | 2 |
-5-
| ||
| 4 |
-1+
| ||
| 2 |
-5-
| ||
| 4 |
-1+
| ||
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com