练习册

  • 练习册
  • 试题
    1 相关关系与函数关系的区别是 2 为了了解名学生对学校某项教改试验的意见.打算从中抽取一个容量为的样 考虑用系统抽样.则分段的间隔为 3 从个篮球中任取一个.检验其质量.则应采用的抽样方法为 4 采用简单随机抽样从含个个体的总体中抽取一个容量为的样本.个体 前两次未被抽到.第三次被抽到的概率为 5 甲.乙两人在相同条件下练习射击.每人打发子弹.命中环数如下 甲 6 8 9 9 8 乙 10 7 7 7 9 则两人射击成绩的稳定程度是 【查看更多】

     

    题目列表(包括答案和解析)

    精英家教网精英家教网（理）已知函数f(x)=
    ln(2-x2)
    |x+2|-2
    ．
    （1）试判断f（x）的奇偶性并给予证明；
    （2）求证：f（x）在区间（0，1）单调递减；
    （3）如图给出的是与函数f（x）相关的一个程序框图，试构造一个公差不为零的等差数列
    {an}，使得该程序能正常运行且输出的结果恰好为0．请说明你的理由．
    （文）如图，在平面直角坐标系中，方程为x2+y2+Dx+Ey+F=0的圆M的内接四边形ABCD的对角线AC和BD互相垂直，且AC和BD分别在x轴和y轴上．
    （1）求证：F＜0；
    （2）若四边形ABCD的面积为8，对角线AC的长为2，且
    AB
    •
    AD
    =0    ，求D2+E2-4F的值；
    （3）设四边形ABCD的一条边CD的中点为G，OH⊥AB且垂足为H．试用平面解析几何的研究方法判
    断点O、G、H是否共线，并说明理由．

    查看答案和解析>>

    弹簧挂着的小球作上下运动，它在t秒时相对于平衡位置的高度h厘米由下列关系式确定：

    ．

    以t为横坐标，h为纵坐标，作出这个函数在一个周期的闭区间上的图象，并回答下列问题：

    (1)小球在开始振动时(即t＝0)的位置在哪里？

    (2)小球的最高点和最低点与平衡位置的距离分别是多少？

    (3)经过多少时间小球往复运动一次？

    (4)每秒钟小球能往复振动多少次？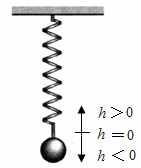

    查看答案和解析>>

    如图，弹簧挂着小球作上下振动，时间t(s)与小球相对于平衡位置(即静止时的位置)的高度h(cm)之间的函数关系式是，t∈[0，＋∞)．以t为横坐标，h为纵坐标，画出这个函数在长度为一个周期的闭区间上的简图，并且回答下列问题：

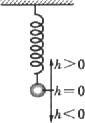
    (1)小球开始振动(t＝0)时位置在哪里？

    (2)小球最高点、最低点与平衡位置的距离分别是多少？

    (3)小球往复振动一次需要多长时间？

    (4)小球每1 s能往复振动多少次？

    查看答案和解析>>

    上海市徐汇区2011届高三下学期学习能力诊断卷（数学理）.doc
     

    （本题满分14分）第（1）小题满分6分，第（2）小题满分8分。

    如图1，，是某地一个湖泊的两条互相垂直的湖堤，线段和曲线段分别是湖泊中的一座栈桥和一条防波堤。为观光旅游的需要，拟过栈桥上某点分别修建与，平行的栈桥、，且以、为边建一个跨越水面的三角形观光平台。建立如图2所示的直角坐标系，测得线段的方程是，曲线段的方程是，设点的坐标为，记。（题中所涉及的长度单位均为米，栈桥和防波堤都不计宽度）

    （1）求的取值范围；

    （2）试写出三角形观光平台面积关于的函数解析式，并求出该面积的最小值。

    查看答案和解析>>

    上海市徐汇区2011届高三下学期学习能力诊断卷（数学理）.doc
     

    （本题满分14分）第（1）小题满分6分，第（2）小题满分8分。

    如图1，，是某地一个湖泊的两条互相垂直的湖堤，线段和曲线段分别是湖泊中的一座栈桥和一条防波堤。为观光旅游的需要，拟过栈桥上某点分别修建与，平行的栈桥、，且以、为边建一个跨越水面的三角形观光平台。建立如图2所示的直角坐标系，测得线段的方程是，曲线段的方程是，设点的坐标为，记。（题中所涉及的长度单位均为米，栈桥和防波堤都不计宽度）

    （1）求的取值范围；

    （2）试写出三角形观光平台面积关于的函数解析式，并求出该面积的最小值。

    查看答案和解析>>


    同步练习册答案