
题目列表(包括答案和解析)
分析:凡是与向量夹角有关的问题,多用数量积公式a·b=|a||b|cosθ来解决,只需求出a·b、|a|2、|b|2,即可转化为实数不等式.
已知向量a=(cosα,sinα),b=(cosβ,sinβ),且a、b满足关系|ka+b|=![]() |a-kb|(k为正实数).
|a-kb|(k为正实数).
(1)求证:(a+b)⊥(a-b);
(2)求将a与b的数量积表示为关于k的函数f(k);
(3)求函数f(k)的最小值及取得最小值时a与b的夹角θ.
(14分)已知向量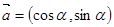 ,
, ,且
,且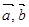 满足关系
满足关系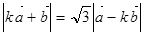 (其中
(其中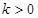 )
)
(1)求证: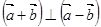
(2)求将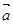 与
与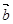 的数量积表示为关于
的数量积表示为关于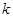 的函数
的函数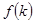 ;
;
(3)求函数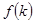 的最小值及取最小值时
的最小值及取最小值时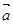 与
与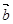 的夹角
的夹角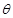
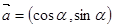 ,
,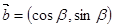 ,且
,且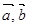 满足关系
满足关系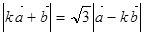 (其中
(其中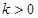 )
)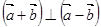
 与
与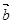 的数量积表示为关于
的数量积表示为关于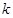 的函数
的函数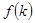 ;
;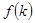 的最小值及取最小值时
的最小值及取最小值时 与
与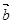 的夹角
的夹角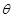
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com