
题目列表(包括答案和解析)
(本小题满分14分)
为了加快县域经济的发展,某县选择两乡镇作为龙头带动周边乡镇的发展,决定在这两个镇的周边修建环形高速公路,假设一个单位距离为![]() ,两镇的中心
,两镇的中心![]() 相距8个单位距离,环形高速公路所在的曲线为
相距8个单位距离,环形高速公路所在的曲线为![]() ,且
,且![]() 上的点到
上的点到![]() 的距离之和为10个单位距离,在曲线
的距离之和为10个单位距离,在曲线![]() 上建一个加油站
上建一个加油站![]() 与一个收费站
与一个收费站![]() ,使
,使![]() 三点在一条直线上,并且
三点在一条直线上,并且![]() 个单位距离.
个单位距离.
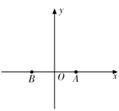 (1) 建立如图的直角坐标系,求曲线
(1) 建立如图的直角坐标系,求曲线![]() 的方程及
的方程及![]() 之间的距离有多少个单位距离;
之间的距离有多少个单位距离;
(2) ![]() 之间有一条笔直公路
之间有一条笔直公路![]() 与X轴正方向成
与X轴正方向成![]() ,且与曲线
,且与曲线![]() 交于
交于![]() 两点,该县招商部门引进外资在四边形
两点,该县招商部门引进外资在四边形![]() 区域开发旅游业,试问最大的开发区域是多少?(平方单位距离)
区域开发旅游业,试问最大的开发区域是多少?(平方单位距离)
(本小题满分14分)
已知![]() ,
,![]() 是双曲线
是双曲线![]() 的左、右焦点,动点
的左、右焦点,动点![]() 到
到![]() ,
,![]() 的距离之和为
的距离之和为![]() ,设动点
,设动点![]() 的轨迹是曲线
的轨迹是曲线![]()
(1)求曲线![]() 的方程;
的方程;
(2)设直线![]() 过
过![]() 与曲线
与曲线![]() 相交于
相交于![]() 、
、![]() 两点,求
两点,求![]() 面积最大时的直线
面积最大时的直线![]() 的方程;
的方程;
(3)设点![]() ,点
,点![]() 是曲线
是曲线![]() 上的两点,
上的两点,![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
|
| ξ |
|
| ξ |
| ξ2 |
| ξ |
|
| π |
| 4 |
| 2 |
| 1 |
| 3 |
(本小题满分14分)
椭圆![]() 上任一点
上任一点![]() 到两个焦点的距离的和为6,焦距为
到两个焦点的距离的和为6,焦距为![]() ,
,![]() 分别是椭圆的左右顶点.
分别是椭圆的左右顶点.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)若![]() 与
与![]() 均不重合,设直线
均不重合,设直线![]() 与
与![]() 的斜率分别为
的斜率分别为![]() ,证明:
,证明:![]() 为定值;
为定值;
(Ⅲ)设![]() 为椭圆上一动点,
为椭圆上一动点,![]() 为
为![]() 关于
关于![]() 轴的对称点,四边形
轴的对称点,四边形![]() 的面积为
的面积为![]() ,设
,设![]() ,求函数
,求函数![]() 的最大值.
的最大值.
.(本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.
如图所示的自动通风设施.该设施的下部 是等腰梯形,其中
是等腰梯形,其中 米,梯形的高为
米,梯形的高为 米,
米, 米,上部
米,上部 是个半圆,固定点
是个半圆,固定点 为
为 的中点.△
的中点.△ 是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),
是由电脑控制其形状变化的三角通风窗(阴影部分均不通风), 是可以沿设施边框上下滑动且始终保持和
是可以沿设施边框上下滑动且始终保持和 平行的伸缩横杆.
平行的伸缩横杆.
(1)设 与
与 之间的距离为
之间的距离为 米,试将三角通风窗
米,试将三角通风窗 的通风面积
的通风面积 (平方米)表示成关于
(平方米)表示成关于 的函数
的函数 ;
;
(2)当 与
与 之间的距离为多少米时,三角通风窗
之间的距离为多少米时,三角通风窗 的通风面积最大?并求出这个最大面积。
的通风面积最大?并求出这个最大面积。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com