
题目列表(包括答案和解析)
(本小题满分14分)
为了加快县域经济的发展,某县选择两乡镇作为龙头带动周边乡镇的发展,决定在这两个镇的周边修建环形高速公路,假设一个单位距离为![]() ,两镇的中心
,两镇的中心![]() 相距8个单位距离,环形高速公路所在的曲线为
相距8个单位距离,环形高速公路所在的曲线为![]() ,且
,且![]() 上的点到
上的点到![]() 的距离之和为10个单位距离,在曲线
的距离之和为10个单位距离,在曲线![]() 上建一个加油站
上建一个加油站![]() 与一个收费站
与一个收费站![]() ,使
,使![]() 三点在一条直线上,并且
三点在一条直线上,并且![]() 个单位距离.
个单位距离.
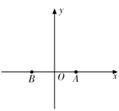 (1) 建立如图的直角坐标系,求曲线
(1) 建立如图的直角坐标系,求曲线![]() 的方程及
的方程及![]() 之间的距离有多少个单位距离;
之间的距离有多少个单位距离;
(2) ![]() 之间有一条笔直公路
之间有一条笔直公路![]() 与X轴正方向成
与X轴正方向成![]() ,且与曲线
,且与曲线![]() 交于
交于![]() 两点,该县招商部门引进外资在四边形
两点,该县招商部门引进外资在四边形![]() 区域开发旅游业,试问最大的开发区域是多少?(平方单位距离)
区域开发旅游业,试问最大的开发区域是多少?(平方单位距离)
(本题满分14分)
如图1,在平面内,ABCD是![]() 的菱形,ADD``A1和CD D`C1都是正方形.将两个正方形分别沿AD,CD折起,使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).
的菱形,ADD``A1和CD D`C1都是正方形.将两个正方形分别沿AD,CD折起,使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).
(Ⅰ) 设二面角E – AC – D1的大小为q,若![]() £ q £
£ q £ ![]() ,求线段BE长的取值范围;
,求线段BE长的取值范围;

(第20题–1)

(第20题–2)
(Ⅱ)在线段![]() 上存在点
上存在点![]() ,使平面
,使平面![]() 平面
平面![]() ,求
,求![]() 与BE之间满足的关系式,并证明:当0 < BE < a时,恒有
与BE之间满足的关系式,并证明:当0 < BE < a时,恒有![]() < 1.
< 1.
(本小题满分14分) 如图,在墙上挂着一块边长为16cm的正方形木板,上面画了小、中、大三个同心圆,半径分别为2cm,4cm,6cm,某人站在3m之外向此板投镖,设投镖击中线上或没有投中木板时都不算(可重投),
 问:(1)投中大圆内的概率是多少?
问:(1)投中大圆内的概率是多少?
(2)投中小圆与中圆形成的圆环的概率是多少?
(3)投中大圆之外的概率是多少?
(本题满分14分)
如图1,在平面内,ABCD是![]() 的菱形,ADD``A1和CD D`C1都是正方形.将两个正方形分别沿AD,CD折起,使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).
的菱形,ADD``A1和CD D`C1都是正方形.将两个正方形分别沿AD,CD折起,使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).
(Ⅰ) 设二面角E – AC – D1的大小为q,若![]() £ q £
£ q £ ![]() ,求线段BE长的取值范围;
,求线段BE长的取值范围;

(第20题–1)

(第20题–2)
(Ⅱ)在线段![]() 上存在点
上存在点![]() ,使平面
,使平面![]() 平面
平面![]() ,求
,求![]() 与BE之间满足的关系式,并证明:当0 < BE < a时,恒有
与BE之间满足的关系式,并证明:当0 < BE < a时,恒有![]() < 1.
< 1.
(本小题满分14分)如图所示,某市政府决定在以政府大楼O为中心、正北方向
和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考
虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正
面要朝市政府大楼.设扇形的半径OM=R ,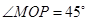 ,OB与OM之间的夹角为
,OB与OM之间的夹角为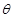 .
.
(1)将图书馆底面矩形ABCD的面积S表示成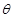 的函数.
的函数.
(2)若 R=45 m,求当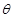 为何值时,矩形ABCD的面积S有最大值?
为何值时,矩形ABCD的面积S有最大值?
其最大值是多少?
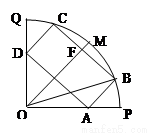
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com