(本小题满分14分)

   如图，已知椭圆的左、右焦点分别为短轴两的端点为A、B，且四边形是边长为2的正方形.

   （Ⅰ）求椭圆的方程；

（Ⅱ）若C、D分别是椭圆长轴的左、右端点，动点M满足MD连结交椭圆于点证明:为定值;

（Ⅲ）在（Ⅱ）的条件下，试问轴上是否存在异于点的定点，使得以为直径的圆恒过直线的交点，若存在，求出点的坐标；若不存在,说明理由.

(本小题满分14分)

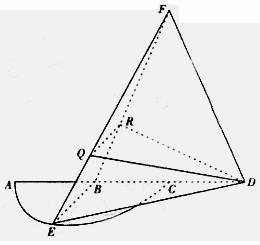如图5，是半径为的半圆，为直径，点为的中点，点和点为线段的三等分点，平面外一点满足，。

（1）证明：；

（2已知点为线段上的点，

，，求平面与平面所成二面角的正弦值。

(本小题满分14分）如图，已知⊙O所在的平面，是⊙O的直径，，

C是⊙O上一点，且，与⊙O所在的平面成角，

是中点．F为PB中点．

(Ⅰ) 求证： ；(Ⅱ) 求证：；

（Ⅲ）求三棱锥B-PAC的体积．

(本小题满分14分)

为了检测某种产品的直径（单位mm），抽取了一个容量为100的样本，其频率分布表（不完整）如下：

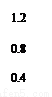
（Ⅰ）完成频率分布表；   

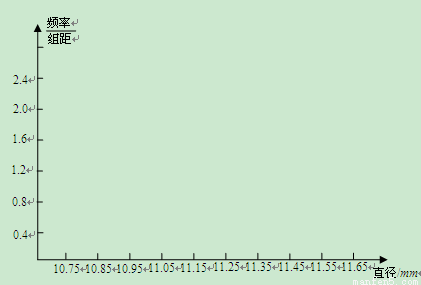
（Ⅱ）画出频率分布直方图；

（Ⅲ）据上述图表，估计产品直径落在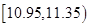范围内的可能性是百分之几？

(本小题满分14分）

如图（1），是直径的上一点，为的切线，为切点，为等边三角形，连接交于，以为折痕将翻折到图（２）的位置．

（1）求证异面直线和互相垂直；

（2）若三棱锥的体积为，求二面角的正弦值．