
题目列表(包括答案和解析)
△ABC中,内角A、B、C成等差数列,其对边a、b、c满足 ,求A。
,求A。
【解析】本试题主要考查了解三角形的运用,
因为

【点评】该试题从整体来看保持了往年的解题风格,依然是通过边角的转换,结合了三角形的内角和定理的知识,以及正弦定理和余弦定理,求解三角形中的角的问题。试题整体上比较稳定,思路也比较容易想,先将利用等差数列得到角B,然后利用余弦定理求解运算得到A。
观察下面两个推理过程及结论:
若锐角 满足
满足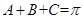 ,以角
,以角 分别为内角构造一个三角形,依据正弦定理和余弦定理可得到等式:
分别为内角构造一个三角形,依据正弦定理和余弦定理可得到等式: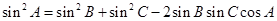 ,
,
若锐角 满足
满足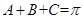 ,则
,则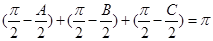 ,以角
,以角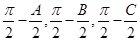 分别为内角构造一个三角形,依据正弦定理和余弦定理可以得到的等式:
分别为内角构造一个三角形,依据正弦定理和余弦定理可以得到的等式: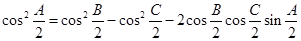 .
.
则:若锐角 满足
满足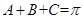 ,类比上面推理方法,可以得到的一个等式是______________.
,类比上面推理方法,可以得到的一个等式是______________.
观察下面两个推理过程及结论:
若锐角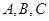 满足
满足 ,以角
,以角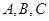 分别为内角构造一个三角形,依据正弦定理和余弦定理可得到等式:
分别为内角构造一个三角形,依据正弦定理和余弦定理可得到等式: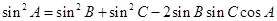 ,
,
若锐角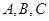 满足
满足 ,则
,则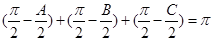 ,以角
,以角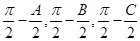 分别为内角构造一个三角形,依据正弦定理和余弦定理可以得到的等式:
分别为内角构造一个三角形,依据正弦定理和余弦定理可以得到的等式: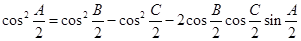 .
.
则:若锐角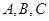 满足
满足 ,类比上面推理方法,可以得到的一个等式是______________.
,类比上面推理方法,可以得到的一个等式是______________.
观察下面两个推理过程及结论:
若锐角 满足
满足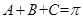 ,以角
,以角 分别为内角构造一个三角形,依据正弦定理和余弦定理可得到等式:
分别为内角构造一个三角形,依据正弦定理和余弦定理可得到等式: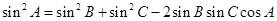 ,
,
若锐角 满足
满足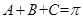 ,则
,则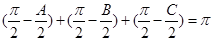 ,以角
,以角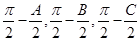 分别为内角构造一个三角形,依据正弦定理和余弦定理可以得到的等式:
分别为内角构造一个三角形,依据正弦定理和余弦定理可以得到的等式: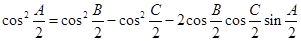 .
.
则:若锐角 满足
满足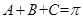 ,类比上面推理方法,可以得到的一个等式是______________.
,类比上面推理方法,可以得到的一个等式是______________.
观察下面两个推理过程及结论:
若锐角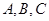 满足
满足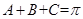 ,以角
,以角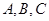 分别为内角构造一个三角形,依据正弦定理和余弦定理可得到等式:
分别为内角构造一个三角形,依据正弦定理和余弦定理可得到等式: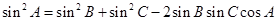 ,
,
若锐角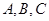 满足
满足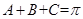 ,则
,则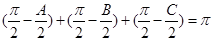 ,以角
,以角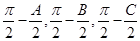 分别为内角构造一个三角形,依据正弦定理和余弦定理可以得到的等式:
分别为内角构造一个三角形,依据正弦定理和余弦定理可以得到的等式: .
.
则:若锐角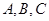 满足
满足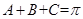 ,类比上面推理方法,可以得到的一个等式是______________.
,类比上面推理方法,可以得到的一个等式是______________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com