
题目列表(包括答案和解析)
给出以下问题:
①求面积为1的正三角形的周长;
②求键盘所输入的三个数的算术平均数;
③求键盘所输入的两个数的最小数;
④求函数 当自变量取
当自变量取 时的函数值.
时的函数值.
其中不需要用条件语句来描述算法的问题有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
为了了解某班学生每周做家务劳动的时间,某综合实践活动小组对该班50名学生进行了调查,有关数据如下表:
| 每周做家务的时间(小时) | 0 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
| 人数(人) | 2 | 2 | 6 | 8 | 12 | 13 | 4 | 3 |
根据上表中的数据,回答下列问题:
(1)该班学生每周做家务劳动的平均时间是多少小时?
(2)这组数据的中位数、众数分别是多少?
(3)请你根据(1)、(2)的结果,用一句话谈谈自己的感受.
(本小题满分12分)学数学,其实是要使人聪明,使人的思维更加缜密,在美国广为流传的一道数学题目是:老板给你两个加工资的方案。一是每年年末加一千元;二是每半年结束时加300元。请选择一种。一般不擅长数学的人很容易选择前者,因为一年加一千元总比两个半年共加600元要多。其实,由于工资累计的,时间稍长,往往第二种方案更有利。例如在第二年的年末,依第一种方案可以加得1000+2000=3000元,而第二种方案在第一年加得300+600=900元,第二年加得900+1200=2100元,总数也是900+2100=3000元。但到了第三年,第一种方案可以得到1000+2000+3000=6000元,第二种方案可以得到300+600+900+1200+1500+1800=6300元,比第一方案多了300元。第四年,第五年会更多。因此,你若会在公司干三年以上,则应选择第二种方案。
根据以上材料,解答以下问题:
(1)如果在该公司干10年,问选择第二方案比选择第一方案多加薪多少元?
(2)如果第二方案中得每半年加300元改成每半年加 ![]() 元,问
元,问 ![]() 取何值时,选 择第二方案总是比选择第一方案多加薪?
取何值时,选 择第二方案总是比选择第一方案多加薪?
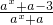 (a>0且a≠1).
(a>0且a≠1). ,求实数a的值.
,求实数a的值.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com