
题目列表(包括答案和解析)
(1)求这批灯泡中“使用时间超过10 800小时”的灯泡的概率;
(2)现从这批灯泡中随机抽取100个,求这100个灯泡中“使用时间超过10 800小时”的灯泡个数的期望.(下列数据供计算时选用:Φ(0.5)=0.691 5,Φ(1)=0.841 3,Φ(2)=0.977 2)
分析:本题考查正态分布与标准正态分布的转化及二项分布的数学期望.
| 1 | ||
|
| (x-80)2 |
| 200 |
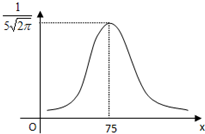 某校某次数学考试的成绩X服从正态分布,其密度函数为f(x)=
某校某次数学考试的成绩X服从正态分布,其密度函数为f(x)=| 1 | ||
|
| (x-μ)2 |
| 2σ2 |
| 等级得分 | (0,1] | (1,2] | (2,3] | (3,4] | (4,5] | (5,6] |
| 人数 | 3 | 17 | 30 | 30 | 17 | 3 |


 |
| y |
| 129 |
| 1 | ||
|
| (x-80)2 |
| 200 |
| A、该市这次考试的数学平均成绩为80分 |
| B、分数在120分以上的人数与分数在60分以下的人数相同 |
| C、分数在110分以上的人数与分数在50分以下的人数相同 |
| D、该市这次考试的数学标准差为10 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com