
题目列表(包括答案和解析)
分别写出下列各组命题构成的“p或q”“p且q”“非p”形式的复合命题:
(1)p:连续的三个整数的乘积能被2整除, q:连续的三个整数的乘积能被3整除.
(2)p:对角线互相垂直的四边形是菱形, q:对角线互相平分的四边形是菱形.
分别写出下列各组命题构成的“p或q”“p且q”“非p”形式的复合命题:
(1)p:![]() 是无理数,q:
是无理数,q: ![]() 大于是2
大于是2
(2)p:![]() ,q:
,q:![]()
(3)p: ![]() , q:
, q: ![]()
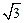 是无理数,q:
是无理数,q: 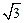 大于是2
大于是2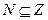 ,q:
,q: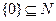
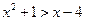 , q:
, q: 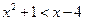
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com