
题目列表(包括答案和解析)
| x2+4 |
| 1 |
| 2 |
| x2+4 |
| x2+4 |
| g(x) |
A.lg(x2y![]() )=(lgx)2+lgy+
)=(lgx)2+lgy+![]() B.lg(x2y
B.lg(x2y![]() )=(lgx)2+lgy+2lgz
)=(lgx)2+lgy+2lgz
C.lg(x2y![]() )=2lgx+lgy-2lgz D.lg(x2y
)=2lgx+lgy-2lgz D.lg(x2y![]() )=2lgx+lgy+
)=2lgx+lgy+![]() lgz
lgz
用反证法证明一个命题时,下列说法正确的是( )
A.将结论与条件同时否定,推出矛盾
B.肯定条件,否定结论,推出矛盾
C.将被否定的结论当条件,经过推理得出结论只与原题条件矛盾,才是反证支的正确运用
D.将被否定的结论当条件,原题的条件不能当条件
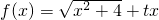 (x∈R)
(x∈R)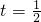 时,可以将f(x)化成
时,可以将f(x)化成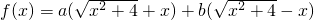 的形式,运用基本不等式求f(x)的最小值及此时x的取值;
的形式,运用基本不等式求f(x)的最小值及此时x的取值;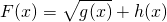 ,利用基本不等式研究函数F(x)的最值问题.
,利用基本不等式研究函数F(x)的最值问题.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com