题目列表(包括答案和解析)
如下图，在四棱锥P－ABCD中，底面ABCD是∠DAB＝60°，且边长为a的菱形．侧面PAD为正三角形，其所在的平面垂直于底面ABCD．
(1)若G为AD边的中点，求证：BG⊥平面PAD．
(2)求证：AD⊥PB．
(3)若E为BC边的中点，能否在棱PC上找到一点F，使平面DEF⊥平面ABCD？证明你的结论．
如下图，在四棱锥P－ABCD中，底面ABCD是一直角梯形，∠BAD＝90°，AD∥BC，AB＝BC＝a，AD＝2a，PA⊥底面ABCD，∠PDA＝30°，AE⊥PD．
试建立适当的空间直角坐标系，并写出各点的坐标．
如下图，在四棱锥P－ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD＝DC，E是PC的中点，作EF⊥PB交PB于点F．
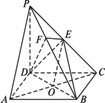
(1)证明PA∥平面EDB；
(2)证明PB⊥平面EFD．
如下图，在四棱锥P－ABCD中，底面是矩形且AD＝2，AB＝PA＝
，PA⊥底面ABCD，E是AD的中点，F在PC上．
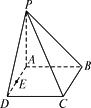
(1)求F在何处时，EF⊥平面PBC；
(2)在(1)的条件下，EF是否是PC与AD的公垂线段，若是，求出公垂线段的长度；若不是，说明理由．
如下图，在四棱锥P－ABCD中，底面ABCD为正方形，PD⊥平面ABCD，且PD＝AB＝a，E是PB的中点．
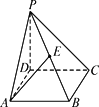
在平面PAD内求一点F，使得EF⊥平面PBC．
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com