
题目列表(包括答案和解析)
某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表:
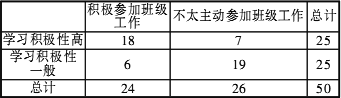
试运用独立性检验的思想分析学生的学习积极性与对待班级工作的态度是否有关系?并说明理由.
①圆的渐开线的参数方程不能转化为普通方程;
②圆的渐开线也可以转化为普通方程,但是转化后的普通方程比较麻烦,且不容易看出坐标之间的关系,所以常使用参数方程研究圆的渐开线问题;
③在求圆的摆线和渐开线方程时,如果建立的坐标系原点和坐标轴选取不同,可能会得到不同的参数方程;
④圆的渐开线和x轴一定有交点而且是唯一的交点.
其中正确的说法有( )
A.①③ B.②④ C.②③ D.①③④
①圆的渐开线的参数方程不能转化为普通方程;
②圆的渐开线也可以转化为普通方程,但是转化后的普通方程比较麻烦,且不容易看出坐标之间的关系,所以常使用参数方程研究圆的渐开线问题;
③在求圆的摆线和渐开线方程时,如果建立的坐标系原点和坐标轴选取不同,可能会得到不同的参数方程;
④圆的渐开线和x轴一定有交点而且是唯一的交点.
其中正确的说法有( )
A.①③
B.②④
C.②③
D.①③④
①圆的渐开线的参数方程不能转化为普通方程;
②圆的渐开线也可以转化为普通方程,但是转化后的普通方程比较麻烦,且不容易看出坐标之间的关系,所以常使用参数方程研究圆的渐开线问题;
③在求圆的摆线和渐开线方程时,如果建立的坐标系原点和坐标轴选取不同,可能会得到不同的参数方程;
④圆的渐开线和x轴一定有交点而且是唯一的交点.
其中正确的说法有( )
A.①③ B.②④
C.②③ D.①③④
(本小题满分12分)
已知双曲线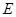 :
: 的左焦点为
的左焦点为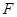 ,左准线
,左准线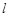 与
与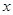 轴的交点是圆
轴的交点是圆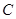 的圆心,圆
的圆心,圆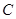 恰好经过坐标原点
恰好经过坐标原点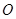 ,设
,设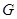 是圆
是圆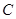 上任意一点.
上任意一点.
(Ⅰ)求圆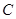 的方程;
的方程;
(Ⅱ)若直线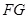 与直线
与直线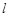 交于点
交于点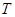 ,且
,且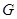 为线段
为线段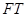 的中点,求直线
的中点,求直线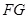 被圆
被圆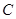 所截得的弦长;
所截得的弦长;
(Ⅲ)在平面上是否存在定点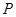 ,使得对圆
,使得对圆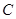 上任意的点
上任意的点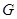 有
有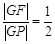 ?若存在,求出点
?若存在,求出点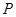 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com