
题目列表(包括答案和解析)
给定精度ε,用二分法求函数f(x)的零点近似值的步骤如下:
A.确定区间[a,b],验证________,给定精度ε;
B.求区间(a,b)的中点x1;
C.计算f(x1);若f(x1)=0,则________就是函数的零点;若f(a)·f(x1)<0,则令________=x1(此时零点x0∈(a,x1));若f(x1)·f(b)<0,则令________=x1(此时零点x0∈(x1,b));
D.判断是否达到精度ε:即若________,则得到零点近似值a(或b);否则重复步骤B~D.
| 2+4 | 2 |
| 2+4 | 2 |
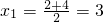 ,计算得f(2)•f(x1)<0,则此时零点x0∈________.(填区间)
,计算得f(2)•f(x1)<0,则此时零点x0∈________.(填区间)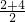 =3,计算得f(2).f(x1)<0,f(x1)•f(4)>0则此时零点x0∈______.(填区间)
=3,计算得f(2).f(x1)<0,f(x1)•f(4)>0则此时零点x0∈______.(填区间)湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com