
题目列表(包括答案和解析)
 如图是一种加热水和食物的太阳灶,上面装有可旋转的抛物面形的反光镜,镜的轴截面是抛物线的一部分,盛水和食物的容器放在抛物线的焦点处,容器由若干根等长的铁筋焊接在一起的架子支撑.已知镜口圆的直径为12 m,镜深2 m,
如图是一种加热水和食物的太阳灶,上面装有可旋转的抛物面形的反光镜,镜的轴截面是抛物线的一部分,盛水和食物的容器放在抛物线的焦点处,容器由若干根等长的铁筋焊接在一起的架子支撑.已知镜口圆的直径为12 m,镜深2 m,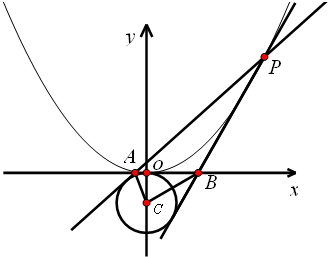 已知抛物线x2=2py(p>0).抛物线上的点M(m,1)到焦点的距离为2
已知抛物线x2=2py(p>0).抛物线上的点M(m,1)到焦点的距离为23
| ||
| 5 |
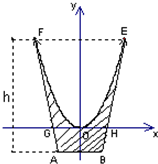 一个特殊模具容器横断面如图所示:内壁是抛物线y=
一个特殊模具容器横断面如图所示:内壁是抛物线y=| 1 |
| 2 |
| 1 |
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com