
题目列表(包括答案和解析)
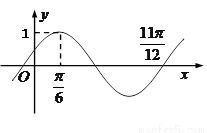
函数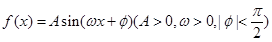 的部分图象如图示,则将
的部分图象如图示,则将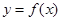 的图象向右平移
的图象向右平移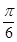 个单位后,得到的图象解析式为 (
)
个单位后,得到的图象解析式为 (
)
A.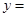
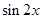 B.
B.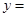
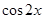
C.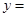
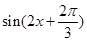 D.
D.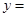
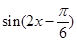
如图,图(1)、(2)、(3)、(4)分别包含1个、5个、13个、25个第二十九届北京奥运会吉祥物“福娃迎迎”,按同样的方式构造图形,设第![]() 个图形包含
个图形包含![]() 个“福娃迎迎”,则
个“福娃迎迎”,则![]() .(答案用
.(答案用![]() 的解析式表示)
的解析式表示)

2.C解析,因为函数f(x)的唯一零点同时在区间(1,3),(1,4),(1,5)内,由此断定这个唯一零点应在(1,3)内,错误的只有C
已知回归直线斜率的估计值为1.23,样本的中心点为(4,5),则回归直线方程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4. m>2或m<-2 解析:因为f(x)=![]() 在(-1,1)内有零点,所以f(-1)f(1)<0,即(2+m)(2-m)<0,则m>2或m<-2
在(-1,1)内有零点,所以f(-1)f(1)<0,即(2+m)(2-m)<0,则m>2或m<-2
随机变量![]() 的所有等可能取值为1,2…,n,若
的所有等可能取值为1,2…,n,若![]() ,则( )
,则( )
A. n=3 B.n=4 C. n=5 D.不能确定
5.m=-3,n=2 解析:因为![]() 的两零点分别是1与2,所以
的两零点分别是1与2,所以![]() ,即
,即![]() ,解得
,解得![]()
6.![]() 解析:因为
解析:因为![]() 只有一个零点,所以方程
只有一个零点,所以方程![]() 只有一个根,因此
只有一个根,因此![]() ,所以
,所以![]()
已知直线![]() 与函数
与函数![]() 的图像的两个相邻交点之间的距离为
的图像的两个相邻交点之间的距离为![]() 。
。
(I)求![]() 的解析式,并求出
的解析式,并求出![]()
![]() 的单调递增区间;
的单调递增区间;
(II)将函数![]() 的图像向左平移
的图像向左平移![]() 个单位得到函数
个单位得到函数![]() 的图像,求函数
的图像,求函数![]() 的最大值及
的最大值及![]() 取得最大值时x的取值集合。
取得最大值时x的取值集合。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com