
题目列表(包括答案和解析)
| 时段 | 峰时(8:00-21:00) | 谷时(21:00-次日8:00) |
| 每千瓦时/元 | 0.5 | 0.3 |
| 交 通 工 具 | 票 价 | 说 明 |
| 火车(硬 卧) | 450元 | 身高1.1m-1.4m的儿童乘坐火车时享受半价票 |
| 飞机(普通舱) | 1500元 | 已满2周岁未满12周岁的儿童乘坐飞机时享受半价票 |
| 住 宿 | 伙 食 | 市 内 交 通 | 旅 游 景 点 门 票 |
| 每日240元(共4天) | 每日100元(共4天) | 每日100元(共4天) | 每人450元 |
| 项目 | 金额(元) |
| 交通费 | 2650 |
| 食宿费 | 1360 |
| 门票费 | 1350 |
| 合计 | 4960 |
叶序现象与斐波那契数列
你吃过菠萝么
?仔细观察菠萝果实的排列状况,就会发现它们形成一种螺旋结构。使人惊异的是,这种排列的现象在植物的叶、鳞片、花等部分,几乎到处可见。再进一步研究一下这些排列的状况,它们通常是以顺时针方向或逆时针方向螺旋形层层排列的。如果数一下其中顺时针和逆时针排列的层数,就可发现这两个数是位于斐波那契数列中相邻的两个数。
什么是斐波那契数列
?斐波那契(1170-1240)是一位意大利的数学家。他在所写的《算盘书》一书中,提出了下面的问题。“有小兔子一对,如果它们第二个月成年,第三个月生下一对小兔,以后,每月生产小兔一对,而所生的小兔亦在第二个月成年,第三个月生产另一对小兔,此后也每个月生一对小兔。则一年后共有多少对兔子
?”(假设每产一对兔子必为一雌一雄,而所有兔子都可以相互交配,并且没有死亡。)
分析:


这样推算下去,每个月所生的兔子数可以排成下面的数列:
1,1,2,3,5,8,13,21,34,55,89,144……
我们把这一列数称为斐波那契数列。研究一下这一列数的规律,从第三项起每一个数都是排在它前面两个数的和。如
2=1+1,3=1+2,5=2+3,8=3+5,13=5+8,21=8+13,…
斐波那契数列可以无限地写下去。设
 表示其中的第n项,那么
表示其中的第n项,那么
 。
。
比如,我们上面排出的第
11项是89,第12项是144,那么第13项应该是

以下各项依序是



… … …
生物学家研究了花序中小花排列的螺旋数,一般顺时针方向为
21,逆时针方向为34,恰恰是斐波那契数列中的 及
及 。又如向日葵花序中小花或籽粒的排列,顺时针螺旋数与逆时针螺旋数之比一般是12∶21(
。又如向日葵花序中小花或籽粒的排列,顺时针螺旋数与逆时针螺旋数之比一般是12∶21( ),34∶55(
),34∶55( ),89∶144(
),89∶144( ),在一些大型样本中,这个比值甚至为144∶233(
),在一些大型样本中,这个比值甚至为144∶233(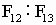 )。同样,生物学家研究了各种菠萝球形花的鳞片顺、逆时针的螺旋数,一般总是落在斐波那契数列3,5,8和13相邻的两数中。
)。同样,生物学家研究了各种菠萝球形花的鳞片顺、逆时针的螺旋数,一般总是落在斐波那契数列3,5,8和13相邻的两数中。
为什么不同的植物都具有类似的螺旋
?为什么这些螺旋圈数总是相邻的斐波那契数?兔子的繁衍与植物的花序之间为什么会有这样的联系,这些问题至今尚未得到令人满意的解答。目前,科学家们一般认为,对植物来说,斐波那契叶序是最节约能量的。叶序现象与斐波那契数列
你吃过菠萝么
?仔细观察菠萝果实的排列状况,就会发现它们形成一种螺旋结构。使人惊异的是,这种排列的现象在植物的叶、鳞片、花等部分,几乎到处可见。再进一步研究一下这些排列的状况,它们通常是以顺时针方向或逆时针方向螺旋形层层排列的。如果数一下其中顺时针和逆时针排列的层数,就可发现这两个数是位于斐波那契数列中相邻的两个数。
什么是斐波那契数列
?斐波那契(1170-1240)是一位意大利的数学家。他在所写的《算盘书》一书中,提出了下面的问题。“有小兔子一对,如果它们第二个月成年,第三个月生下一对小兔,以后,每月生产小兔一对,而所生的小兔亦在第二个月成年,第三个月生产另一对小兔,此后也每个月生一对小兔。则一年后共有多少对兔子
?”(假设每产一对兔子必为一雌一雄,而所有兔子都可以相互交配,并且没有死亡。)
分析:


这样推算下去,每个月所生的兔子数可以排成下面的数列:
1,1,2,3,5,8,13,21,34,55,89,144……
我们把这一列数称为斐波那契数列。研究一下这一列数的规律,从第三项起每一个数都是排在它前面两个数的和。如
2=1+1,3=1+2,5=2+3,8=3+5,13=5+8,21=8+13,…
斐波那契数列可以无限地写下去。设
 表示其中的第n项,那么
表示其中的第n项,那么
 。
。
比如,我们上面排出的第
11项是89,第12项是144,那么第13项应该是

以下各项依序是



… … …
生物学家研究了花序中小花排列的螺旋数,一般顺时针方向为
21,逆时针方向为34,恰恰是斐波那契数列中的 及
及 。又如向日葵花序中小花或籽粒的排列,顺时针螺旋数与逆时针螺旋数之比一般是12∶21(
。又如向日葵花序中小花或籽粒的排列,顺时针螺旋数与逆时针螺旋数之比一般是12∶21( ),34∶55(
),34∶55( ),89∶144(
),89∶144( ),在一些大型样本中,这个比值甚至为144∶233(
),在一些大型样本中,这个比值甚至为144∶233( )。同样,生物学家研究了各种菠萝球形花的鳞片顺、逆时针的螺旋数,一般总是落在斐波那契数列3,5,8和13相邻的两数中。
)。同样,生物学家研究了各种菠萝球形花的鳞片顺、逆时针的螺旋数,一般总是落在斐波那契数列3,5,8和13相邻的两数中。
为什么不同的植物都具有类似的螺旋
?为什么这些螺旋圈数总是相邻的斐波那契数?兔子的繁衍与植物的花序之间为什么会有这样的联系,这些问题至今尚未得到令人满意的解答。目前,科学家们一般认为,对植物来说,斐波那契叶序是最节约能量的。在下面的
( )里填上适当的长度单位.(km、m、dm、cm、mm).(1)
数学书宽约2( ).(2)
珠穆朗玛峰是世界上最高的山峰,海拔约9( ).在下面的
( )里填上适当的长度单位.(km、m、dm、cm、mm).(1)
数学书宽约2( ).(2)
珠穆朗玛峰是世界上最高的山峰,海拔约9( ).湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com