
题目列表(包括答案和解析)
已知直线AB∥CD,直线EF与AB、CD分别相交于点E、F.

(1)如图1,若∠1=60°,求∠2、∠3的度数;
(2)若点P是平面内的一个动点,连结PE、PF,探索∠EPF、∠PEB、∠PFD三个角之间的关系:
①当点P在图2的位置时,可得∠EPF=∠PEB+∠PFD;
请阅读下面的解答过程,并填空(理由或数学式).
解:如图2,过点P作MN∥AB,
则∠EPM=∠PEB______
∵AB∥CD(已知),MN∥AB(作图),
∴MN∥CD______
∴∠MPF=∠PFD______
∴______=∠PEB+∠PFD(等式的性质)
即∠EPF=∠PEB+∠PFD.
②当点P在图3的位置时,请直接写出∠EPF、∠PEB、∠PFD三个角之间的关系:______;
③当点P在图4的位置时,请直接写出∠EPF、∠PEB、∠PFD三个角之间的关系:______.
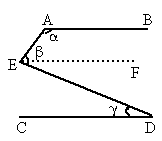
已知,如图,AB∥CD,则图中α、β、γ三个角之间的数量关系为
[ ]
A.α+β+γ=360°
B.α+β+γ=180°
C.α+β-γ=180°
D.α-β-γ=90°
已知:如图,在□ABCD中,O为对角线BD的中点.过O的直线MN交直线AB于点M,交直线CD于点N;过O的另一条直线PQ交直线AD于点P,交直线BC于点Q,连结PN、MQ.
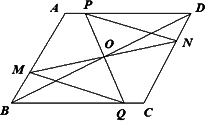
(1)试证明△PON与△QOM全等;
(2)若点O为直线BD上任意一点,其他条件不变,则△PON与△QOM又有怎样的关系?试就点O在如图所示的位置,画出图形,证明你的猜想;

(3)若点O为直线BD上任意一点(不与点B、D重合),设OD∶OB=k,PN=x,MQ=y,则y与x之间的函数关系式为________.
 (如图(3)),试求EG的长度.
(如图(3)),试求EG的长度.
 (如图(3)),试求EG的长度.
(如图(3)),试求EG的长度.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com