练习册

  • 练习册
  • 试题
    (三)用9.8.6.5组成最大的四位数9865和最小的四位数5689 (1)9865-5689= 中所得的四位数各个数位上的数字组成一个最 大数减去最小数.得到一个新的四位数. (3)对于新得到的四位数.重复上面的过程.你发现了什么? (4) 任选一个四位数(各个数位上的数字都不相等).重复上面的过程.你有什么新的发现吗? 三 试一试 1.一支考古队在某地挖掘出一枚正方体的古代金属印章.其棱长为4.5厘米.质量为1069克.求这枚印章每立方厘米约重多少克? 2.有人说“如果把一张纸对折一次.再对折一次.如此重复下去.第43次后所有纸的高度相当于地球到月球的距离. 已知一张纸的厚度是0.006厘米.地球到月球的距离大约是385 000千米. 你相信这个人的说法吗? 3 P83 【查看更多】

     

    题目列表(包括答案和解析)

    数学游戏：
    【游戏一】有一种数字游戏，操作步骤如下：
    第一步，任意写一个自然数（以下简称为原数，原数中至少有一个偶数数字）；
    第二步，再写一个新三位数，它的百位数字是原数中偶数数字的个数，十位数字是原数中奇数数字的个数，个位数是原数的位数；
    以下每一步都对上一步得到的数，按照第二步的规则进行操作，直到这个数不再变化为止．请求出这个数．
    【游戏二】任意写出一个数字不全相同的四位数，用这个数的各个数位上的数字连同它的符号分别组成最大的数和最小的数，计算所组成的最大数与最小数的差．再对所得的差重复上述操作，直到这个数不再变化为止．请求出这个数．

    查看答案和解析>>

    任意写出一个数字不全相同的4位数，用这个数中的4个数字连同它的符号分别组成最大的数和最小的数，计算所组成的最大数与最小数的差[例如：－1023．用1、0、2、3及“－”号组成的最大数为－123(即“－0123”)，最小数为－3210，作差，得－123－(－3210)＝3087]．再对所得的差重复上述操作，结果如何？请与同学交流．

    查看答案和解析>>

    用总长为32m的篱笆墙围成一个扇形的花园．
    （1）试写出扇形花园的面积y（m2）与半径x（m）之间的函数关系式和自变量x的取值范围；
    （2）用描点法作出函数的图象；
    （3）当扇形花园半径为多少时，花园面积最大？最大面积是多少？此时这个扇形的圆心角是多大（精确到0.1度）？
    （4）请回答：如果同样用32m的篱笆围成一个面积最大的矩形花园，这个花园的面积是多少？对比上面的结论，你有什么发现？

    查看答案和解析>>

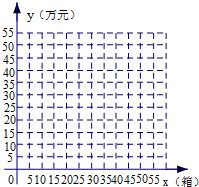    宜万铁路开通后，给恩施州带来了很大方便．恩施某工厂拟用一节容积是90立方米、最大载重量为50吨的火车皮运输购进的A、B两种材料共50箱．已知A种材料一箱的体积精英家教网是1.8立方米、重量是0.4吨；B种材料一箱的体积是1立方米、重量是1.2吨；不计箱子之间的空隙，设A种材料进了x箱．
    （1）求厂家共有多少种进货方案（不要求列举方案）？
    （2）若工厂用这两种材料生产出来的产品的总利润y（万元）与x（箱）的函数关系大致如下表，请先根据下表画出简图，猜想函数类型，求出函数解析式（求函数解析式不取近似值），确定采用哪种进货方案能让厂家获得最大利润，并求出最大利润．
    x 15 20 25 30 38 40 45 50
    y 10 约27.58 40 约48.20 约49.10 约47.12 40 约26.99

    查看答案和解析>>

    （2010•北海）如图，在△OAB中，AO=AB，∠OAB=90°，点B坐标为（10，0）．过原点O的抛物线，又过点A和G，点G坐标为（7，0）．
    （1）求抛物线的解析式；
    （2）边OB上一动点T（t，0），（T不与点O、B重合）过点T作OA、AB的垂线，垂足分别为C、D．设△TCD的面积为S，求S的表达式（用t表示），并求S的最大值；
    （3）已知M（2，0），过点M作MK⊥OA，垂足为K，作MN⊥OB，交点OA于N．在线段OA上是否存在一点Q，使得Rt△KMN绕点Q旋转180°后，点M、K恰好落在（1）所求抛物线上？若存在请求出点Q和抛物线上与M、K对应的点的坐标，若不存在请说明理由．

    查看答案和解析>>


    同步练习册答案