25、有一个“猜成语”游戏，其规则是：参加游戏的每两个人一组，主持人出示一块写有成语的牌子给两个人中的一人（甲）看，但是另一个（乙）是看不到牌子上的成语的?现在我们把这个游戏中的成语改成两个整数，要求甲用一句话或者一个式子、一个图形告诉乙这两个数（同样要求不能出现与牌子上相同的数字）?如果你是甲，对于下面两个数：“-1和1”将怎样告诉乙？（至少说出两种）
你的解答是
方法一：
方法二：

（2012•新区二模）在图形的全等变换中，有旋转变换，翻折（轴对称）变换和平移变换．一次数学活动课上，老师组织大家利用矩形进行图形变换的探究活动．
（1）第一小组的同学发现，在如图1-1的矩形ABCD中，AC、BD相交于点O，Rt△ADC可以由Rt△ABC经过一种变换得到，请你写出这种变换的过程．

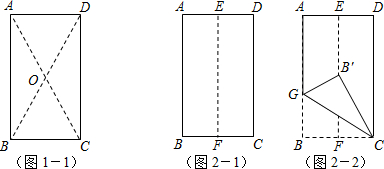
（2）第二小组同学将矩形纸片ABCD按如下顺序进行操作：对折、展平，得折痕EF（如图2-1）；再沿GC折叠，使点B落在EF上的点B′处（如图2-2），这样能得到∠B′GC的大小，你知道∠B′GC的大小是多少吗？请写出求解过程．
（3）第三小组的同学，在一个矩形纸片上按照图3-1的方式剪下△ABC，其中BA=BC，将△ABC沿着直线AC的方向依次进行平移变换，每次均移动AC的长度，得到了△CDE、△EFG和△GHI，如图3-2．已知AH=AI，AC长为a，现以AD、AF和AH为三边构成一个新三角形，已知这个新三角形面积小于15

15

，请你帮助该小组求出a可能的最大整数值．

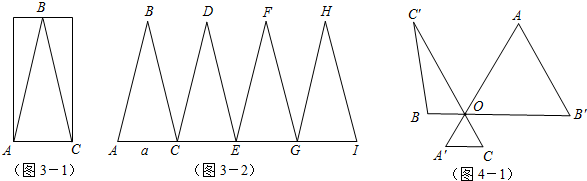
（4）探究活动结束后，老师给大家留下了一道探究题：
如图4-1，已知AA′=BB′=CC′=2，∠AOB′=∠BOC′=∠COA′=60°，请利用图形变换探究S_△AOB′+S_△BOC′+S_△COA′与

3

的大小关系．

你玩过七巧板吗？那是我国古代人民创造的，流传到世界上不少国家．
“七巧板”也称“七巧图”，由七块不同形状的木板组成．七巧板的制作非常简单，下面教你一种方法．把分成七部分的正方形复写在厚纸板上，然后把它割开．七巧板游戏将利用这7个部件，拼出如图所列出的许多图案．或许你能想出自己的图案来？

在七巧板里，7个部件中已经有3种不同尺寸的三角形，用其中的4个部件：1个大三角形、2个小三角形和1个正方形还能拼出1个三角形，你能试试吗？
想一想：
（1）七巧板的2块部件能组成一个三角形吗？3块呢？5块呢？6块呢？7块呢？
（2）用2块部件能组成正方形吗？3块呢？
（3）用哪些部件能组成长方形？还能组成什么样的多边形？