题目列表(包括答案和解析)
如图，∠B＝∠D，∠1＝∠2．求证：AB∥CD．
【证明】∵ ∠1＝∠2（已知），
∴ ∥ （ ），
∴ ∠DAB＋∠ ＝180°（ ）．
∵ ∠B＝∠D（已知），
∴ ∠DAB＋∠ ＝180°（ ），
∴ AB∥CD（ ）．
视图填空．
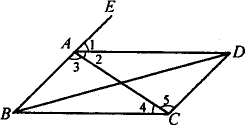
如图，∠1＝∠ABC＝∠ADC，∠3＝∠5，∠2＝∠4，∠ABC＋∠BCD＝180°(1)因为∠1＝∠ABC( )
所以AD∥________( )
(2)因为∠3＝∠5( )
所以AB∥________( )
(3)因为∠2＝∠4(已知)
所以________∥________( )
(4)因为∠1＝∠ADC( )
所以________∥________( )
(5)因为∠ABC＋∠BCD＝180°
所以________∥________( )
( )×(－2
)＝1；(－
)－( )＝－2；(－73)________27＝－46；(－2
)________(－1
)＝2．
填空(如图)
(1)∵∠1＝∠2(已知)
∴________∥________．( )
(2)∵∠1＝∠3(已知)
∴________∥________．( )
(3)∵∠3＋________＝180°
∴________∥________．( )．
A.M＝8，a=8 B.M＝2，a=9 C.M＝8，a=10 D.M＝5，a=10
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com