
题目列表(包括答案和解析)
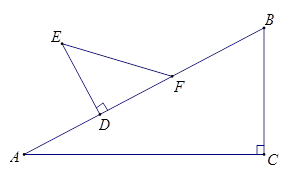
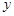 与
与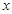 之间的函数关系式及其定义域.
之间的函数关系式及其定义域.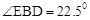 ?如果存在,求出AD的长度;如果不存在,请说明理由.
?如果存在,求出AD的长度;如果不存在,请说明理由.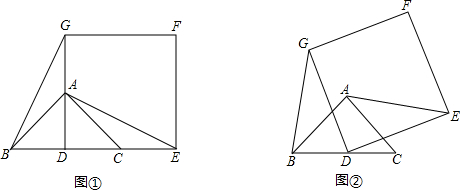

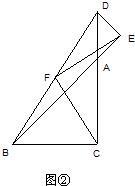
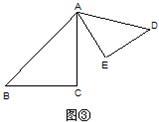
 操作:
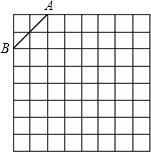
操作: 19、如图:△ABC是一块直角三角形余料,∠C=90度,工人师傅把它加工成一个正方形零件,使C为正方形的一个顶点,其余三个顶点分别在AB、BC、AC边上,请你协助工人师傅用尺规画出裁割线.(不写画法,保留作图痕迹)
19、如图:△ABC是一块直角三角形余料,∠C=90度,工人师傅把它加工成一个正方形零件,使C为正方形的一个顶点,其余三个顶点分别在AB、BC、AC边上,请你协助工人师傅用尺规画出裁割线.(不写画法,保留作图痕迹)湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com