
题目列表(包括答案和解析)
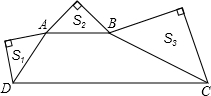 如图,梯形ABCD中,AB∥CD,∠ADC+∠BCD=90°,以AD、AB、BC为斜边向外作等腰直角三角形,其面积分别为S1,S2,S3,且S1+S3=4S2,若将梯形上底AB沿BC方向平移至下底CD上的CE处,连AE,则下列结论:
如图,梯形ABCD中,AB∥CD,∠ADC+∠BCD=90°,以AD、AB、BC为斜边向外作等腰直角三角形,其面积分别为S1,S2,S3,且S1+S3=4S2,若将梯形上底AB沿BC方向平移至下底CD上的CE处,连AE,则下列结论: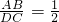 ;④
;④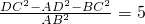 .
. 件,才能使之成立?以下四种改法:
件,才能使之成立?以下四种改法: b>0,则a2>b2;
b>0,则a2>b2; )若a>b且a+b>0,则a2>b2;
)若a>b且a+b>0,则a2>b2; 个
个 如图,二次函数![]() 的图象开口向上,图象经过点(-1,2)和(1,0),且与
的图象开口向上,图象经过点(-1,2)和(1,0),且与![]() 轴相交于负半轴.
轴相交于负半轴.

(
以下有(1)、(2)两问,每个考生只须选答一问,若两问都答,则只以第(2)问计分)第(1)问:给出四个结论:① ![]() ;②
;② ![]() ;③
;③ ![]() ;
;
④ ![]() .其中正确结论的序号是
(答对得3分,少选、错选均不得分).
.其中正确结论的序号是
(答对得3分,少选、错选均不得分).
第(2)问:给出四个结论:① ![]() ;②
;② ![]() ;③
;③ ![]() ;④
;④![]() .其中正确结论的序号是
(答对得5分,少选、错选均不得分).
.其中正确结论的序号是
(答对得5分,少选、错选均不得分).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com