
题目列表(包括答案和解析)
| b |
| a |
| c |
| a |
| b |
| a |
| c |
| a |
| b |
| 2a |
| b |
| a |
| c |
| a |
| b |
| 2a |
| b |
| 2a |
| b2-4ac |
| 4a2 |
| b |
| 2a |
|
-b±
| ||
| 2a |
-b+
| ||
| 2a |
-b-
| ||
| 2a |
 x+
x+ =0,第一步
=0,第一步 x=-
x=- ,第二步
,第二步 )2,得x2+
)2,得x2+ x+2=-
x+2=- +(
+( )2,第三步
)2,第三步 )2=
)2= 直接开方得x+
直接开方得x+ =±
=± ,第四步
,第四步 ,
,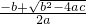 ,x2=
,x2=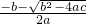 ,第五步
,第五步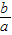 x+
x+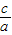 =0,第一步
=0,第一步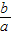 x=-
x=-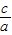 ,第二步
,第二步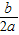 )2,得x2+
)2,得x2+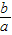 x+( )2=-
x+( )2=-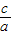 +(
+(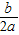 )2,第三步
)2,第三步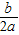 )2=
)2=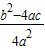 直接开方得x+
直接开方得x+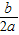 =±
=±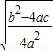 ,第四步
,第四步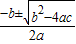 ,
,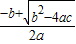 ,x2=
,x2=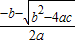 ,第五步
,第五步在学习了一元一次方程的解法以后,陈老师给同学们出了这样一道练习题,解方程
解:去分母,得
4(2x-1)=1-3(x+2).①去括号,得
8x-4=1-3x-6.②移项,得
8x+3x=1-6+4.③合并同类项,得
11x=-1.④两边同除以
11,得x=-陈老师说:吴欢对解一元一次方程的一般步骤是知道的,但没有完全掌握,因此解题时有一步出现了错误,请同学们指出他错在第
________步(填编号),并写出正确的解题过程.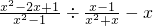 ,其中x=2007”甲同学把“x=2007”错抄成“x=2070”,但他计算的结果也是正确的,你说这是怎么一回事?
,其中x=2007”甲同学把“x=2007”错抄成“x=2070”,但他计算的结果也是正确的,你说这是怎么一回事?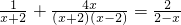

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com