
题目列表(包括答案和解析)
万州新世纪在2011年1至10月份的时间销售A、B两种电子产品,已知产品A每个月的售价y(元)与月份x(1≤x≤10,且为整数)之间的关系可用如下表格表示:
![]()
已知产品A的进价为140元/件,产品A的销量Z(件)与月份x之间的关系是z=20x;已知产品B的进价为450元/件,产品B的售价m(元)与月份x之间的关系是m=-20x+750,产品B的销量p(件)与月份x的关系可用如下的图形反映.
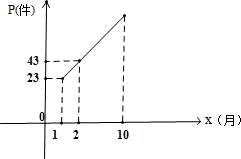
已知该商店每个月需固定支出500元得物管杂费以及5个员工的工资,已知员工每人每月的工资为1500元,请结合上述信息解答下列问题:
(1)请观察表格与图像,用我们所学习的一次函数、反比例函数写出y与x的函数关系式,p与x的函数关系式;
(2)试表示出商店每月销售A、B两种产品的总利润W与月份x的关系式,并求出该商店在哪个月时获得最大利润?
(3)为了鼓励员工的积极性,在最后4个月的销售期间商店老板决定奖励员工,除了正常工资外,每卖一件A产品,每个员工都提成0.75元;每卖一件B产品,每个员工都提成10元,而B产品的销量将每月增加15x件,请问在第几月时总利润可达到16750元?(参考数据:![]() ,
,![]() )
)
阅读材料:
(1)对于任意两个数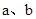 的大小比较,有下面的方法:
的大小比较,有下面的方法:
当 时,一定有
时,一定有 ;
;
当 时,一定有
时,一定有 ;
;
当 时,一定有
时,一定有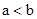 .
.
反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”.
(2)对于比较两个正数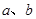 的大小时,我们还可以用它们的平方进行比较:
的大小时,我们还可以用它们的平方进行比较:
∵ ,
,
∴( )与(
)与( )的符号相同
)的符号相同
当 >0时,
>0时,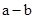 >0,得
>0,得
当 =0时,
=0时,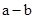 =0,得
=0,得
当 <0时,
<0时,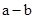 <0,得
<0,得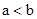
解决下列实际问题:
(1)课堂上,老师让同学们制作几种几何体,张丽同学用了3张A4纸,7张B5纸;李明同学用了2张A4纸,8张B5纸.设每张A4纸的面积为x,每张B5纸的面积为y,且x>y,张丽同学的用纸总面积为W1,李明同学的用纸总面积为W2.回答下列问题:
①W1= (用x、y的式子表示)
W2= (用x、y的式子表示)
②请你分析谁用的纸面积最大.
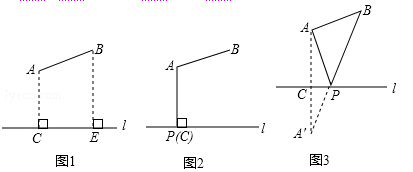
(2)如图1所示,要在燃气管道l上修建一个泵站,分别向A.B两镇供气,已知A.B到l的距离分别是3km、4km(即AC=3km,BE=4km),AB=xkm,现设计两种方案:
方案一:如图2所示,AP⊥l于点P,泵站修建在点P处,该方案中管道长度a1=AB+AP.
方案二:如图3所示,点A′与点A关于l对称,A′B与l相交于点P,泵站修建在点P处,该方案中管道长度a2=AP+BP.
①在方案一中,a1= km(用含x的式子表示);
②在方案二中,a2= km(用含x的式子表示);
③请你分析要使铺设的输气管道较短,应选择方案一还是方案二.
阅读材料:
(1)对于任意两个数 的大小比较,有下面的方法:
的大小比较,有下面的方法:
当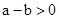 时,一定有
时,一定有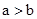 ;
;
当 时,一定有
时,一定有 ;
;
当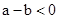 时,一定有
时,一定有 .
.
反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”.
(2)对于比较两个正数 的大小时,我们还可以用它们的平方进行比较:
的大小时,我们还可以用它们的平方进行比较:
∵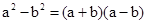 ,
,
∴( )与(
)与( )的符号相同
)的符号相同
当 >0时,
>0时, >0,得
>0,得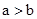
当 =0时,
=0时, =0,得
=0,得
当 <0时,
<0时, <0,得
<0,得
解决下列实际问题:
(1)课堂上,老师让同学们制作几种几何体,张丽同学用了3张A4纸,7张B5纸;李明同学用了2张A4纸,8张B5纸.设每张A4纸的面积为x,每张B5纸的面积为y,且x>y,张丽同学的用纸总面积为W1,李明同学的用纸总面积为W2.回答下列问题:
①W1= (用x、y的式子表示)
W2= (用x、y的式子表示)
②请你分析谁用的纸面积最大.
(2)如图1所示,要在燃气管道l上修建一个泵站,分别向A.B两镇供气,已知A.B到l的距离分别是3km、4km(即AC=3km,BE=4km),AB=xkm,现设计两种方案:

方案一:如图2所示,AP⊥l于点P,泵站修建在点P处,该方案中管道长度a1=AB+AP.
方案二:如图3所示,点A′与点A关于l对称,A′B与l相交于点P,泵站修建在点P处,该方案中管道长度a2=AP+BP.
①在方案一中,a1= km(用含x的式子表示);
②在方案二中,a2= km(用含x的式子表示);
③请你分析要使铺设的输气管道较短,应选择方案一还是方案二.
 阅读材料:(1)对于任意两个数
阅读材料:(1)对于任意两个数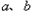 的大小比较,有下面的方法:当
的大小比较,有下面的方法:当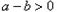 时,一定有
时,一定有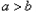 ;当
;当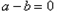 时,一定有
时,一定有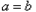 ;当
;当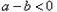 时,一
时,一 定有
定有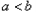 .反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”.
.反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”. 的大小时,我们还可以用它们的平方进行比较:
的大小时,我们还可以用它们的平方进行比较: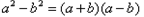 ,
,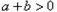
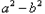 )与(
)与(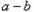 )的符号相同
)的符号相同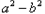 >0时,
>0时,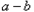 >0,得
>0,得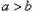
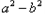 =0时,
=0时,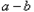 =0,得
=0,得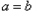
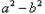 <0时,
<0时,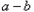 <0,得
<0,得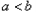
万州新世纪在2011年1至10月份的时间销售A、B两种电子产品,已知产品A每个月的售价y(元)与月份x(![]() ,且为整数)之间的关系可用如下表格表示:
,且为整数)之间的关系可用如下表格表示:
| 时间x(月) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 售价y(元) | 720 | 360 | 240 | 180 | 144 | 120 | 1 | 120 | 120 | 120 |
已知产品A的进价为140元/![]() 件,产品A的销量Z(件)与月份x之间的关系是z=20x;已知产品B的进价为450元/件,产品B的售价m(元)与月份x之间的关系是m=-20x+750,产品B的销量p(件)与月份x的关系可用如下的图形反映。
件,产品A的销量Z(件)与月份x之间的关系是z=20x;已知产品B的进价为450元/件,产品B的售价m(元)与月份x之间的关系是m=-20x+750,产品B的销量p(件)与月份x的关系可用如下的图形反映。
已知该商店每个月需固定支出500元得物管杂费以及5个员工的工![]() 资,已知员工每人每月的工资为1500元,请结合上述信息解答下列问题:
资,已知员工每人每月的工资为1500元,请结合上述信息解答下列问题:
(1)请观察表格与图像,用我们所学习的一次函数、反比例函数写出y与x的函数关系式,p与x的函数关系式;
(2)试表示出商店每月销售A、B两种产品的总利润W与月份x的关系式,并![]() 求出该商店在哪个月时获得最大利润?
求出该商店在哪个月时获得最大利润?
(3)为了鼓励员工的积极性,在最后4个月的销售期间商店老板决定奖励员工,除了正常工资外,每卖一件A产品,每个员工都提成0.75元;每卖一件B产品,每个员工都提成10元,而B产品的销量将每月增加15x件,请问在第几月时总利润可达到16750元?(参考数据:![]() ,
,![]() )
)

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com