
题目列表(包括答案和解析)
(本题满分12分)学完二次函数后,同学们对二次函数的图象抛物线产生了浓厚兴趣,在一次数学实验课上,孔明同学用一把宽3 cm且带刻度的矩形直尺对抛物线进行了如下测量:
①量得OA=3 cm;
②把直尺的左边与抛物线的对称轴重合,使得直尺左下端点与抛物线的顶点重合(如图①),测得抛物线与直尺右边的交点C的刻度读数为4.5.
请完成下列问题:
1.(1)求抛物线的对称轴.
2.(2)求抛物线所对应的函数关系式.
3.(3)将图中的直尺(足够长)沿水平方向向右平移到点A的右边(如图②),直尺的两边交x轴于点H、G,交抛物线于点E、F.求证:S梯形EFGH=![]() (EF2-9).
(EF2-9).

(本题满分12分)学完二次函数后,同学们对二次函数的图象抛物线产生了浓厚兴趣,在一次数学实验课上,孔明同学用一把宽3 cm且带刻度的矩形直尺对抛物线进行了如下测量:
①量得OA=3 cm;
②把直尺的左边与抛物线的对称轴重合,使得直尺左下端点与抛物线的顶点重合(如图①),测得抛物线与直尺右边的交点C的刻度读数为4.5.
请完成下列问题:
1.(1)求抛物线的对称轴.
2.(2)求抛物线所对应的函数关系式.
3.(3)将图中的直尺(足够长)沿水平方向向右平移到点A的右边(如图②),直尺的两边交x轴于点H、G,交抛物线于点E、F.求证:S梯形EFGH= (EF2-9).
(EF2-9).

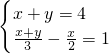
 -
- =1
=1 -
- =1,
=1, =
= -1,
-1, =
=

 代入③得y=4-
代入③得y=4- =3
=3
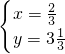 .
. ,y=3
,y=3 代入①得,左边=x+y=
代入①得,左边=x+y= +3
+3 =4,右边=4.
=4,右边=4. ,y=3
,y=3 代入②得
代入②得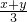 -
- =
=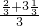 -
-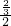 =
= -
- =1,右边=1.
=1,右边=1.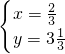 是原方程组的解.
是原方程组的解. 观察猜想
观察猜想为了测量校园内一棵不可攀的树的高度,学校数学应用实践小组做了如下的探索
实践一:根据《自然科学》中的反射定律,利用一面镜子和一根皮尺,设计如图8的测量方案:
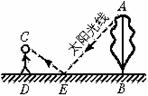
把镜子放在离树(AB)8.7米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.7米,观察者目高CD=1.6米,请你计算树(AB)的高度(精确到0.1米).
实践二:提供选用的测量工具有:①皮尺一根;②教学用三角板一副;③长为2.5米的标杆一根;④高度为1.5米的测角仪(能测量仰角、俯角的仪器)一架.请根据你所设计的测量方案,回答下列问题:
(1)在你设计的方案中,选用的测量工具是(用工具的序号填写)______;
(2)在图1中画出你的测量方案示意图;
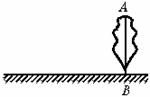
图1
(3)你需要测得示意图中哪些数据,并分别用a、b、c、a 等表示测得的数据______;
(4)写出求树高的算式:AB=_________________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com