练习册

  • 练习册
  • 试题
    因为题目中只是问“马 所在的位置,所以我们只要考虑“马 的位置变化规律就可以了.“马 最开始在2号位置,我们记做②,那么变化规律为: ② ④ ③ ① ② --很容易看出,每交换一次位置,“马 就按顺时针方向转动一格,所以每交换四次,“马 就可以回到原地.因为20¸4=5正好整除,说明“马 正好转了5圈回到原地.所以交换二十次位置后,“马 仍在2号小格内. 【查看更多】

     

    题目列表(包括答案和解析)

    把下列各数填在相应的集合内：

    －3，2，－1，－，－0.58，0，－3.1415926，0.618，．

    整数集合：{　　…}；

    分数集合：{　　…}；

    负数集合：{　　…}；

    非负数集合：{　　…}．

    (题目中只是具体地填出几个符合条件的数，只是一部分，所以通常最后要加省略号)

    查看答案和解析>>

    阅读下面的解题过程，然后解答后面的问题．

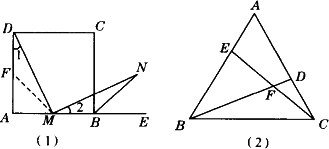
    　　题目：如图(1)，已知正方形ABCD中，点M是AB的中点，点E是AB延长线上的一点，MN⊥DM交∠CBE的平分线BN于点N．试说明MD＝MN．

    　　解：在AD上取一点F，使AF＝AM，连结MF．

    　　因为ABCD是正方形，

    　　所以DF＝MB，∠1＋∠AMD＝90°．

    　　因为DM⊥MN，

    　　所以∠AMD＋∠2＝90°．

    　　所以∠1＝∠2．

    　　因为BN平分∠CBE，

    　　所以∠MBN＝135°＝∠DFM．

    　　所以△DFM≌△MBN．

    　　所以DM＝MN．

    (1)在上述说理过程中，“点M是AB的中点”这个条件没有用到，若将这个条件改为“点M是AB上的任意一点”，或“点M是AB延长线上的任意一点”，或“点M是BA延长线上的任意一点”，则结论“DM＝MN”还成立吗？请说明理由；

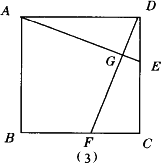
    (2)如图(2)，在正三角形ABC中，若AE＝CD，则∠BFE＝60°；如图(3)，在正方形ABCD中，若DE＝CF，则∠AGF＝90°．这里的两个结论“∠BFE＝60°”和“∠AGF＝90，分别与题目的背景条件“正三角形ABC”和“正方形ABCD”有关．你能否改编一道题目，改变上述题目的背景“正方形ABCD”，并相应改变条件“MN⊥DM”，而其余条件与结论不变？请说明所编题目的正确性．

    查看答案和解析>>

    5、如图所示，小敏做《典中点》中的试题时，不小心把题目中的三角形用墨水弄污了一部分，她想在一块白纸上作一个完全一样的三角形，然后粘贴在上面，她作图的依据是（　　）

    查看答案和解析>>

    7、阅读下面“平均数”一课的课堂教学片断，请你作简单评述．
    师：学到这里，我们已经基本掌握了求平均数的一般方法．其实，在求平均数前，我们还可以先估算这个平均数的范围．请大家看这样一个例子：“一个小组有6个同学，他们的体重分别是32千克、30千克、35千克、30千克、33千克、32千克，这个小组的平均体重是多少千克？”
    仔细想一想，这个小组同学的平均体重肯定比多少千克多，比多少千克少？
    生1：比30千克多，比35千克要少．
    生2：我也认为是这样的．
    师：为什么呢？我们能否说出一个道理？
    学生同桌或小组进行讨论．
    师：谁先发言？
    生：因为求6个同学的平均体重，可以看成是“以多补少”，就是要把最重的35千克移一些给最轻的30千克．所以这个平均数肯定不会比35千克多，比30千克少．
    师：（带头鼓掌，学生也跟着鼓掌）说得好．请大家计算出结果，再与刚才的估算的平均数范围对照一下，是否对？
    生：（学生各自计算：（32+30+35+30+33+32）÷6=32（千克））
    师：好．这个结果说明我们刚才估算的结果是正确的．那么这个“32千克”与题目中的“32千克”意思一样吗？
    生：不一样．题目中的“32千克”是一个同学的体重，结果中的“32千克”是6个同学的平均体重．
    师：说得对！我们解答应用题，不但要会，而且要懂得解答结果的意思．

    查看答案和解析>>

    下列说法正确个数是（　　）
    ①x2=1是一元二次方程；
    ②2x2=2（x-1）（x-1）是一元二次方程；
    ③x2+
    1
    x
    =2不是一元二次方程，因为左边x2+
    1
    x
    不是整式；
    ④2x2-x-y=1不是一元二次方程，因为方程中含有两个未知数x，y．
    A、4个B、3个C、2个D、1个

    查看答案和解析>>


    同步练习册答案