
题目列表(包括答案和解析)
(本题12分)如图,∠AOB为直角,∠BOC为锐角,且OM平分∠AOC,ON平分∠BOC.
1.⑴若∠BOC=50°,试求∠MON的度数;
2.⑵如果⑴中的∠BOC=α(α为锐角),其他条件不变,试求∠MON的度数;
3.⑶如果⑴中∠AOB=β,其他条件不变,你能求出∠MON的度数吗?
4.⑷从⑴⑵⑶的结果,你能看出什么规律?

在平面直角坐标系中,如果抛物线y=2x2不动,而把x轴、y轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式是
A.y=2(x-2)2 + 2 B.y=2(x + 2)2-2
C.y=2(x-2)2-2 D.y=2(x + 2)2 + 2
【提出问题】
如图①,在梯形ABCD中,AD//BC,AC、BD交于点E,∠BEC=n°,若AD=a,BC=b,则梯形ABCD的面积最大是多少?
【探究过程】
小明提出:可以从特殊情况开始探究,如图②,在梯形ABCD中,AD//BC,AC⊥BD,若AD=3,BC=7,则梯形ABCD的面积最大是多少?
如图③,过点D做DE//AC交BC的延长线于点E,那么梯形ABCD的面积就等于△DBE的面积,求梯形ABCD的面积最大值就是求△DBE的面积最大值.如果设AC=x,BD=y,那么S△DBE=xy.
以下是几位同学的对话:
A同学:因为y= ,所以S△DBE=x
,所以S△DBE=x ,求这个函数的最大值即可.
,求这个函数的最大值即可.
B同学:我们知道x2+y2=100,借助完全平方公式可求S△DBE=xy的最大值
C同学:△DBE是直角三角形,底BE=10,只要高最大,S△DBE就最大,我们先将所有满足BE=10的直角△DBE都找出来,然后在其中寻找高最大的△DBE即可.

(1)请选择A同学或者B同学的方法,完成解题过程.
(2)请帮C同学在图③中画出所有满足条件的点D,并标出使△DBE面积最大的点D1.(保留作图痕迹,可适当说明画图过程)
【解决问题】
根据对特殊情况的探究经验,请在图①中画出面积最大的梯形ABCD的顶点D1,并直接写出梯形ABCD面积的最大值.
反比例函数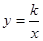 的图象如图所示,点M是该函数图象上一点,MN⊥x轴,垂足是点N,如果S△MON=2,则k的值为( )
的图象如图所示,点M是该函数图象上一点,MN⊥x轴,垂足是点N,如果S△MON=2,则k的值为( )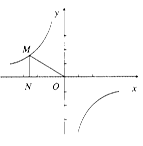
| A.2 | B.-2 | C.4 | D.-4 |
如图,在△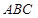 中,
中,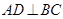 ,
,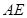 平分∠
平分∠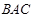 ,∠
,∠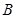 =70°,∠
=70°,∠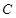 =30°.
=30°.
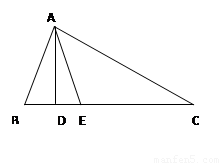
1.求∠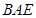 的度数;
的度数;
2.求∠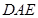 的度数;
的度数;
3.探究:如果只知道∠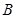 =∠
=∠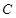 + 40°,也能得出∠
+ 40°,也能得出∠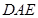 的度数?你认为可以吗?
的度数?你认为可以吗?
若能,请你写出求解过程;若不能,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com