
题目列表(包括答案和解析)
 如图是一个转盘被等分成了4份,自由转动转盘,停止后指针指向黄色区域的概率是( )
如图是一个转盘被等分成了4份,自由转动转盘,停止后指针指向黄色区域的概率是( )A、
| ||
B、
| ||
C、
| ||
| D、不确定 |
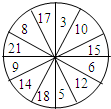 22、如图,一个转盘被平均分成12份,每份上写上不同的数字,游戏方法:先猜数后转动转盘,若指针指向的数字与所猜的数一致,则猜数者获胜.现提供三种猜数方法:
22、如图,一个转盘被平均分成12份,每份上写上不同的数字,游戏方法:先猜数后转动转盘,若指针指向的数字与所猜的数一致,则猜数者获胜.现提供三种猜数方法: 27、如图甲,正方形被划分成16个全等的三角形,将其中若干个三角形涂黑,且满足下列条件:
27、如图甲,正方形被划分成16个全等的三角形,将其中若干个三角形涂黑,且满足下列条件: 如图,一个转盘被等分成6个小扇形.在转盘上涂上适当的颜色,使得自由转动的这个转盘停止转动时,分别满足下列条件:
如图,一个转盘被等分成6个小扇形.在转盘上涂上适当的颜色,使得自由转动的这个转盘停止转动时,分别满足下列条件: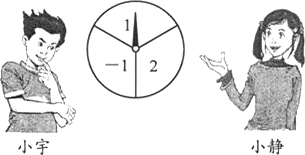
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com