
题目列表(包括答案和解析)
对于关于x的一元二次方程ax2+bx+c=0(a≠0),如果a+b+c=0,那么它的两个根分别为x1=1,x2=![]() .说明如下:
.说明如下:
由于a+b+c=0,则c=-a-b
将c=-a-b代入原方程,得ax2+bx-a-b=0.
即a(x2-1)+b(x-1)=0,所以(x-1)(ax+a+b)=0
解得x1=1,x2=![]() .
.
请利用上面推导出来的结论,快速求解下列方程:
(1)3x2-5x+2=0,x1=________,x2=________;
(2)7x2-4x-3=0,x1=________,x2=________;
(3)13x2+7x-20=0,x1=________,x2=________;
(4)x2-(![]() +1)x+
+1)x+![]() =0,x1=________,x2=________;
=0,x1=________,x2=________;
(5)2004x2-2003x-1=0,x1=________,x2=________;
(6)(b-c)x2+(c-a)x+(a-b)=0(b≠c),x1=________,x2=________;
(7)请你写出3个一元二次方程,使它们都有一个根是1.
已知:一元二次方程![]() .
.
(1)求证:不论k为何实数时,此方程总有两个实数根;
(2)设k<0,当二次函数![]() 的图象与x轴的两个交点A、B间的距离为4时,求此二次函数的解析式;
的图象与x轴的两个交点A、B间的距离为4时,求此二次函数的解析式;
(3)在(2)的条件下,若抛物线的顶点为C,过y轴上一点M(0,m)作y轴的垂线l,当m为何值时,直线l与△ABC的外接圆有公共点?
如图,在△ABC中,∠B=45°,BC=5,高AD=4,矩形EFPQ的一边QP在BC边上,E、F分别在AB、AC上,AD交EF于点H.

(1)求证:![]() ;
;
(2)设EF=x,当x为何值时,矩形EFPQ的面积最大?并求出最大面积;
(3)当矩形EFPQ的面积最大时,该矩形EFPQ以每秒1个单位的速度沿射线DA匀速向上运动(当矩形的边PQ到达A点时停止运动),设运动时间为t秒,矩形EFPQ与△ABC重叠部分的面积为S,求S与t的函数关系式,并写出t的取值范围.
如图,□ABCD在平面直角坐标系中,AD=6,若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB.
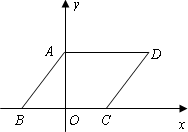
(1)求sin∠ABC的值.
(2)若E为x轴上的点,且![]() ,求经过D、E两点的直线的解析式,并判断△AOE与△DAO是否相似?
,求经过D、E两点的直线的解析式,并判断△AOE与△DAO是否相似?
(3)若点M在平面直角坐标系内,则在直线AB上是否存在点F,使以A、C、F、M为顶点的四边形为菱形?若存在,请直接写出F点的坐标;若不存在,请说明理由.
如图,在平面直角坐标系中,四边形ABCD是平行四边形,AD=6,若OA、OB的长是关于x的一元二次方程 的两个根,且OA>OB.
的两个根,且OA>OB.
(1)求OA、OB的长;
(2)若点E为x轴上的点,且S△AOE= ,求经过D、E两点的直线解析式,并判断△AOE与△AOD是否相似;
,求经过D、E两点的直线解析式,并判断△AOE与△AOD是否相似;
(3)若点M在平面直角坐标系内,则在直线AB上是否存在点F,使以A、C、F、M为顶点的四边形为菱形?若存在,直接写出F点的坐标,若不存在,请说明理由.
如图,在平面直角坐标系中,四边形ABCD是平行四边形,AD=6,若OA、OB的长是关于x的一元二次方程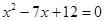 的两个根,且OA>OB.
的两个根,且OA>OB.
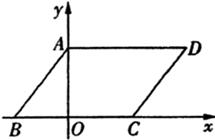
(1)求OA、OB的长;
(2)若点E为x轴上的点,且S△AOE=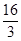 ,求经过D、E两点的直线解析式,并判断△AOE与△AOD是否相似;
,求经过D、E两点的直线解析式,并判断△AOE与△AOD是否相似;
(3)若点M在平面直角坐标系内,则在直线AB上是否存在点F,使以A、C、F、M为顶点的四边形为菱形?若存在,直接写出F点的坐标,若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com